La transformation d'énergie mécanique en énergie électrique, et inversement, ainsi que la conversion de l'énergie électrique reposent sur l'emploi des matériaux magnétiques.
Ces matériaux sont utilisés dans la fabrication des transformateurs électriques, des moteurs électriques, des alternateurs, tant dans l'industrie automobile que dans l'industrie de production de l'énergie électrique, et, pour un grand nombre d' appareils électroménagers.
Le présent article propose quelques notions élémentaires d'électromagnétisme et les effets sur les matériaux utilisés dans la construction des moteurs électriques, des alternateurs ou des transformateurs.
Sommaire
- Matériaux magnétiques:
- Relations de base de l'électromagnétisme:
- Courbe d'aimantation:
- Champ magnétique dans un matériau quelconque:
- Cycle d'hystérésis:
- Flux d'induction magnétique:
- Pertes dans les matériaux magnétiques:
- Grandeurs d'influence :
- Classification des différents matériaux magnétiques :
- Analogie électricité - magnétisme:
- Conclusion
Matériaux magnétiques:
Tout corps métallique pur réagit différemment lorsqu'il est soumis à un champ magnétique. On distingue trois catégories de corps:
>Les corps ferromagnétiques: ces sont des matériaux qui s'aimantent très fortement en présence d'un champ magnétique (comme par exemple le fer, ou le nickel).
>Les corps paramagnétiques: ce type de matériaux s'aimante faiblement en présence d'un champ magnétique (par exemple: l'aluminium, ou le platine).
>Les corps diamagnétiques: ce type de corps s'aimante en sens inverse du champ magnétique, mais très faiblement (par exemple: l'or, l'argent,le plomb, le cuivre).
Relations de base de l'électromagnétisme:
Lorsqu'un courant électrique circule dans un conducteur, il y a création d'un champ magnétique au voisinage de ce conducteur.
Cas d'une bobine longue:
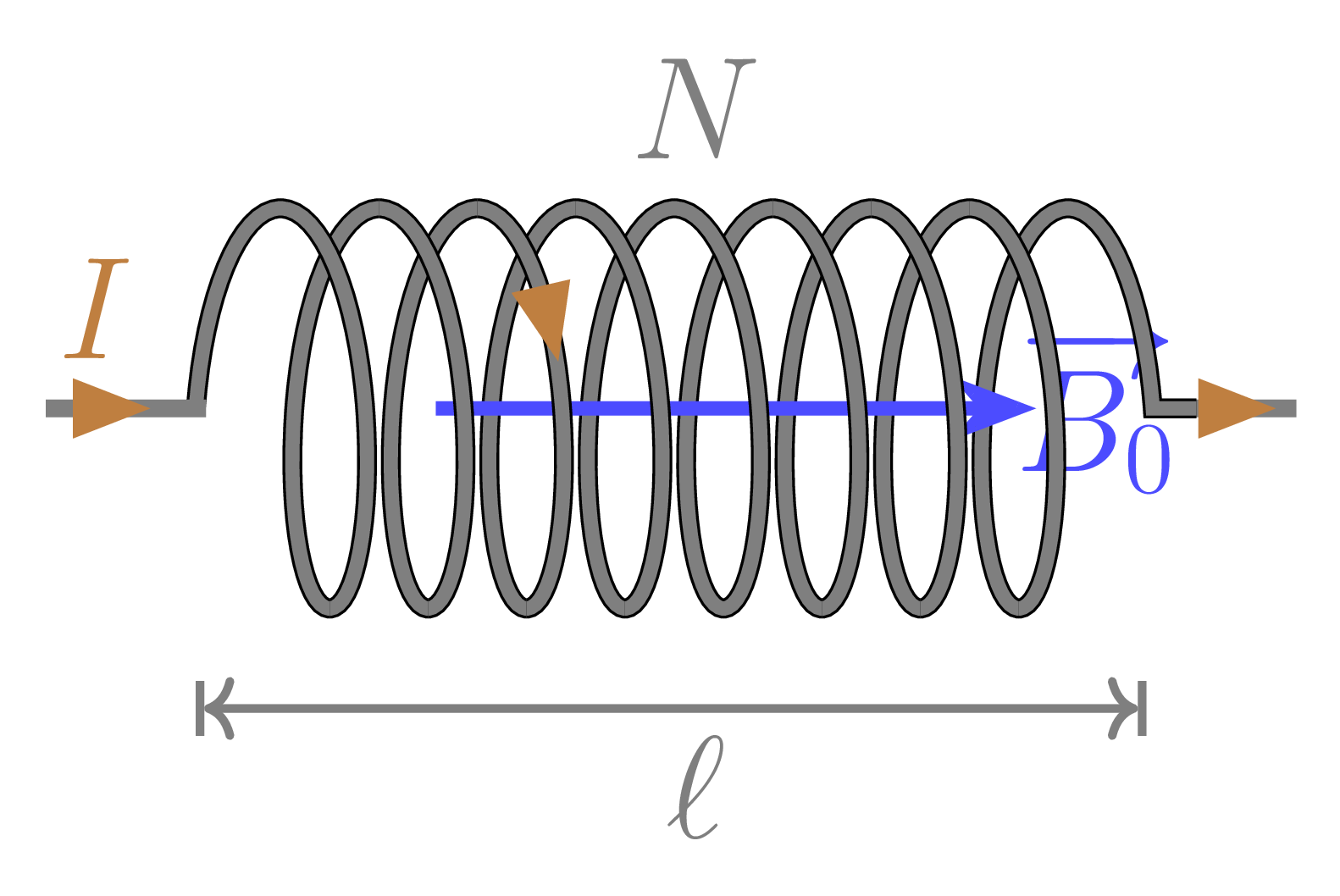
figure - 1
> L'excitation magnétique:
\[\mathsf{H = \frac{N.I}{\ell}}\]
H: excitation magnétique en ampères par mètre (A/m); N: nombre de tours des enroulements ou nombre de spires; I: intensité du courant électrique en ampères (A); \(\ell\): la longueur en mètres (m).
> Le champ magnétique dans l'air ou induction magnétique:
\[\mathsf{B_0 = \frac{\mu_0.N.I}{\ell}}\]
B0: champ magnétique dans l'air en Tesla (T); µ0 : constante magnétique définissant la perméabilité magnétique de l'air = 4.\(\pi\).10-7.
Ainsi on peut écrire:
\[\mathsf{B_0=\mu_0.H}\]
Courbe d'aimantation:
Lorsqu'on augmente l'excitation magnétique H dans une bobine à noyau magnétique fait d'un matériau quelconque (voir figure-2):
Le champ mesuré B varie selon une courbe appelée courbe de première aimantation.
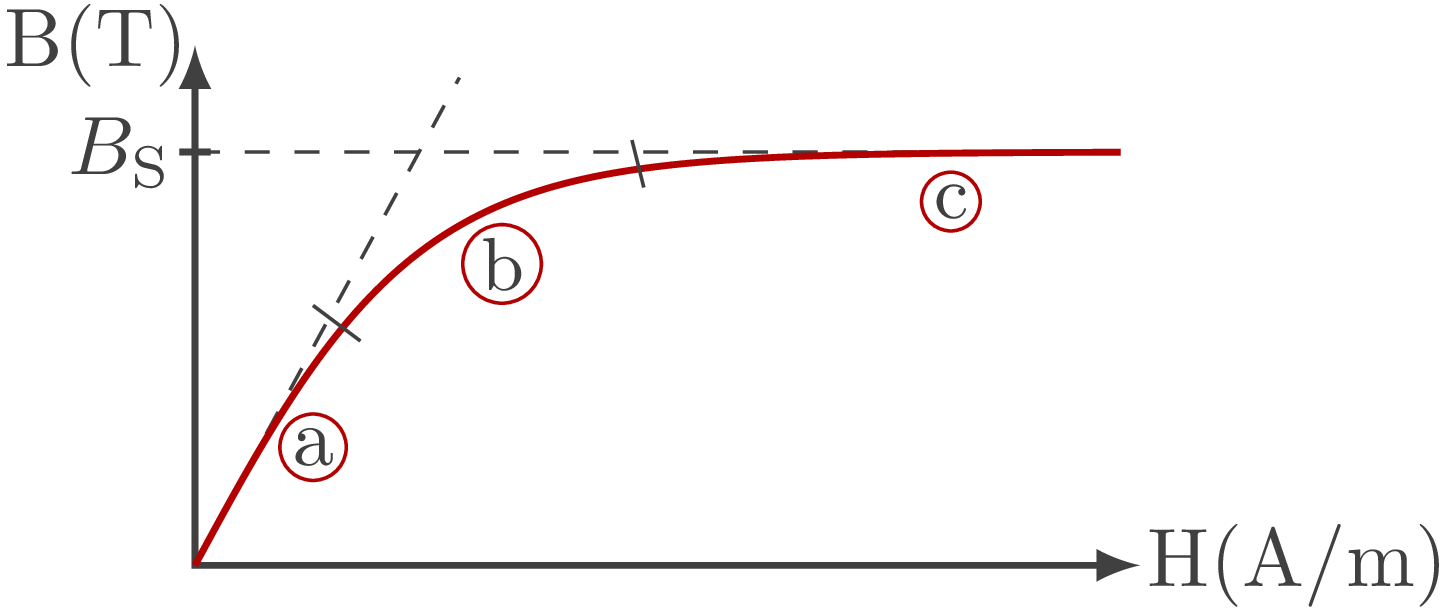
figure - 2
La zone \(\large{\enclose{circle}{a}}\) correspond à la zone de linéarité; H et B varient proportionnellement.
La zone \(\large{\enclose{circle}{b}}\) amorce la saturation; H et B ne varient plus proportionnellement, c'est le coude de saturation;
La zone \(\large{\enclose{circle}{c}}\) correspond à la zone de saturation.
L'allure de cette courbe dépend de la catégorie du matériau utilisé:
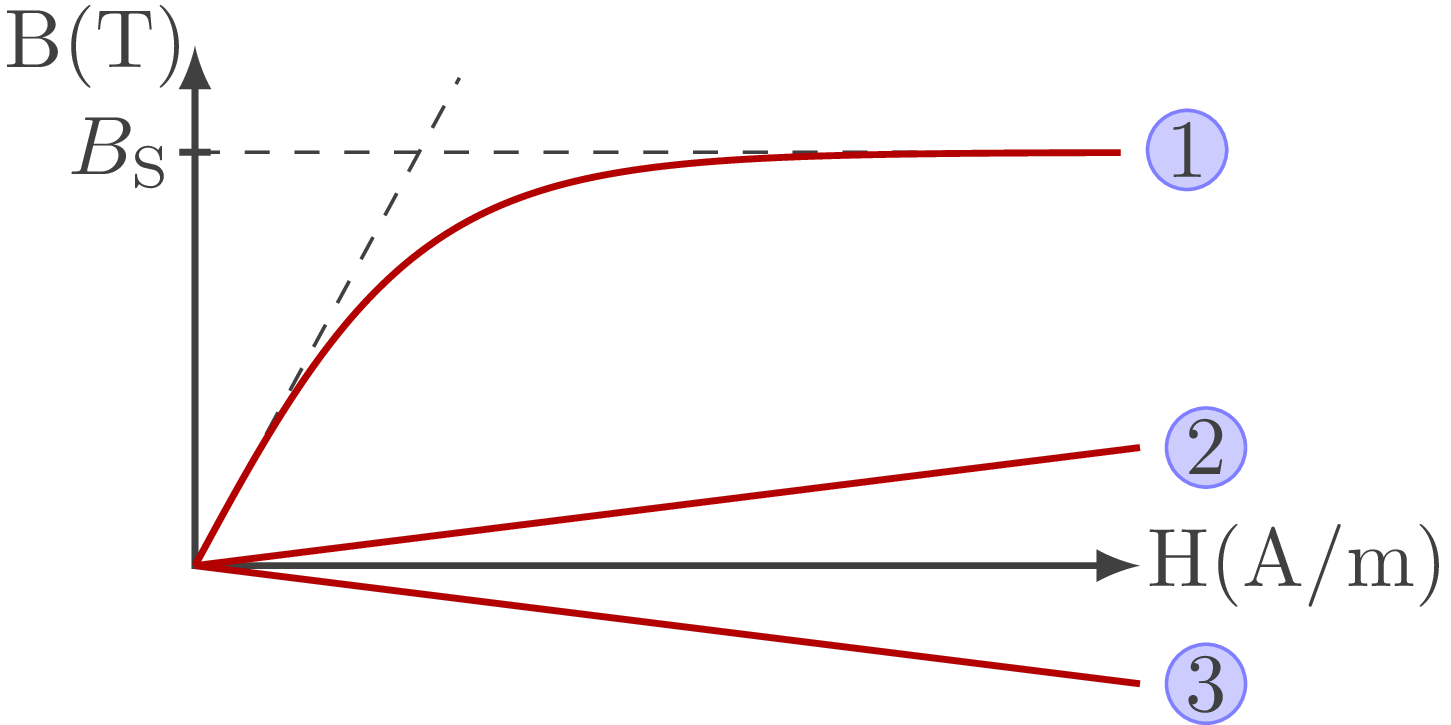
figure-3
La courbe \(\enclose{circle}{1}\) correspond aux matériaux ferromagnétiques.
La courbe \(\enclose{circle}{2}\) correspond aux matériaux paramagnétiques.
La courbe \(\enclose{circle}{3}\) correspond aux matériaux diamagnétiques.
Champ magnétique dans un matériau quelconque:
Dans le cas d'une bobine ayant un noyau constitué d'un matériau quelconque (voir figure-4):
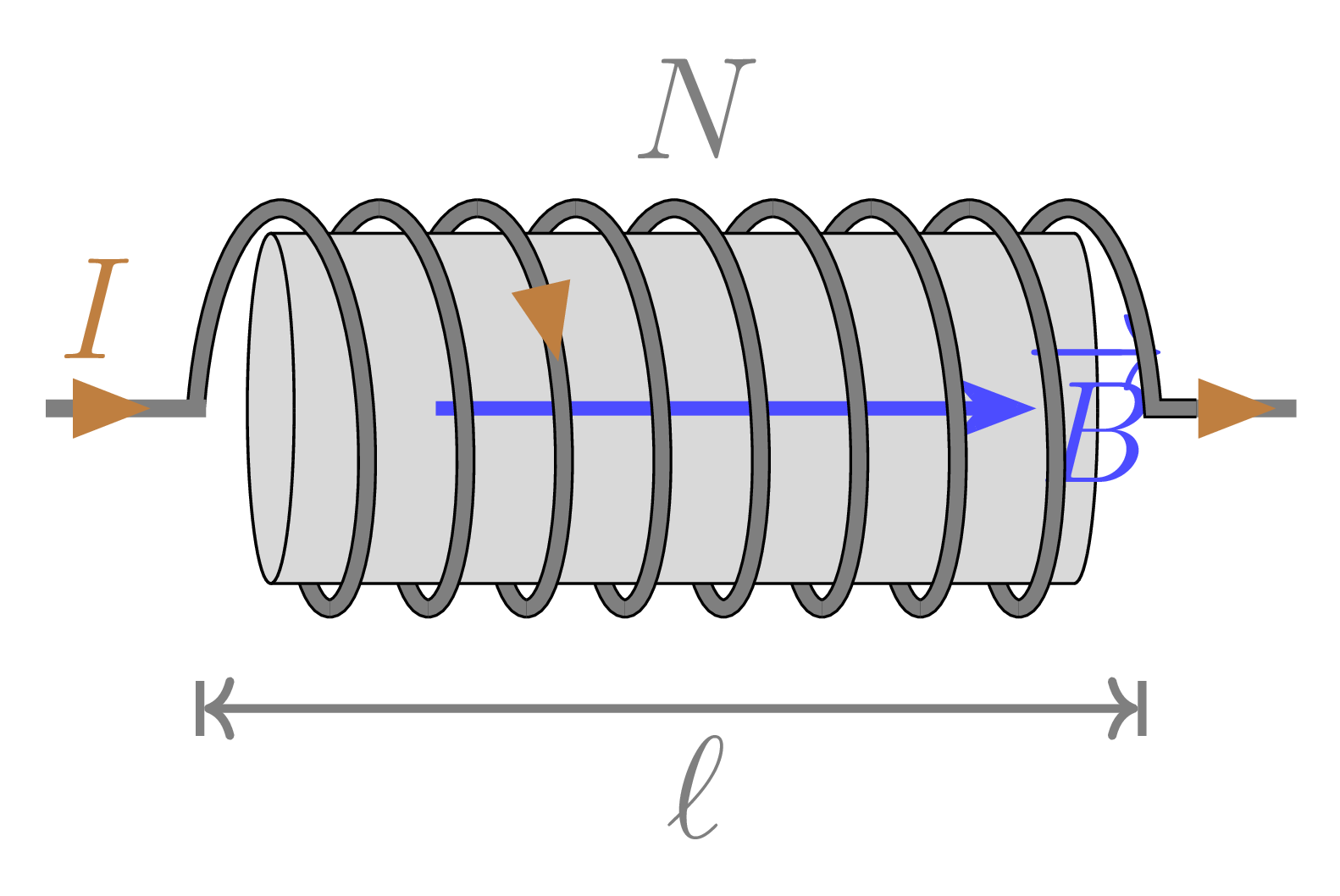
figure-4
On définit:
> La perméabilité relative du matériau par rapport à l'air: cette notion indique combien de fois l'induction est plus grande dans un corps (ou une substance donnée) que dans l'air. Elle est considérée comme étant égale au rapport entre B et B0; noté:
\[\mathsf{\frac{B}{\,B_0}=\mu_r}\]
\(\mu _r\): perméabilité relative du matériau par rapport à l'air.
>La perméabilité absolue du matériau est égale à:
\[\mathsf{\mu = \mu_r.\mu_0}\]
\(\mu\): perméabilité absolue du matériau;
\(\mu_r\): perméabilité relative du matériau;
\(\mu_0\) = 4.\(\pi\).10-7.
> Le champ magnétique dans un matériau quelconque est :
\[\mathsf{B = \mu. H}\]
B: champ magnétique en Tesla (T);
H: excitation magnétique en Ampères par mètre (A/m);
\(\mu\): la perméabilité absolue du matériau.
Cycle d'hystérésis:
Si on soumet un matériau ferromagnétique à un champ dont l'intensité varie entre deux limites; on constate que l'aimantation positive et négative du matériau sont réversibles, mais ne suivent pas la même trajectoire. La courbe B=f(H) ainsi obtenue est appelée cycle d'hystérésis du matériau:
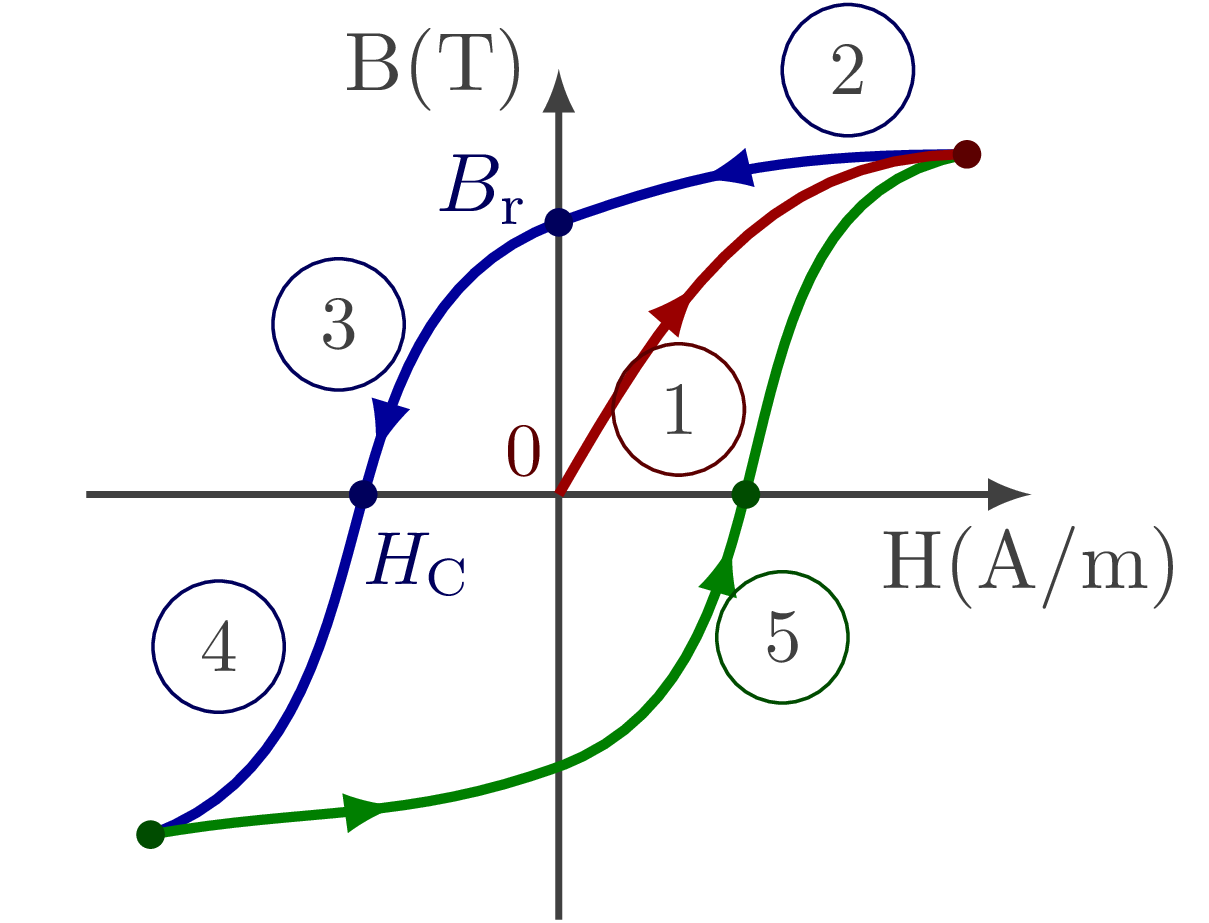
figure-5
Dans ce diagramme:
La courbe \(\enclose{circle}{1}\) représente la courbe de première aimantation
\(\enclose{circle}{2}\) : représente la désaimantation.
\(\enclose{circle}{3}\) : correspond à l'inversion du courant d'aimantation.
\(\enclose{circle}{4}\) : point de départ de l'aimantation en sens inverse.
La partie \(\enclose{circle}{5}\) correspond à la fermeture du cycle.
> \(B_r\), le champ magnétique rémanent: c'est la valeur de l'induction lorsque l'excitation est nulle.
> \(H_c\), l'excitation coercitive: c'est la valeur d'excitation magnétique nécessaire pour que l'induction ou le champ magnétique soit nul.
Cette courbe représente les caractéristiques magnétiques du matériau, en quelque sorte une photo d'identité magnétique. La figure ci-après donne des allures de cycles d'hystérésis de trois matériaux (\(\enclose{circle}{1}\): le fer pur, \(\enclose{circle}{2}\): l'acier au silicium, \(\enclose{circle}{3}\): l'acier dur pour aimants), permettant de définir ainsi leur type d'emploi.
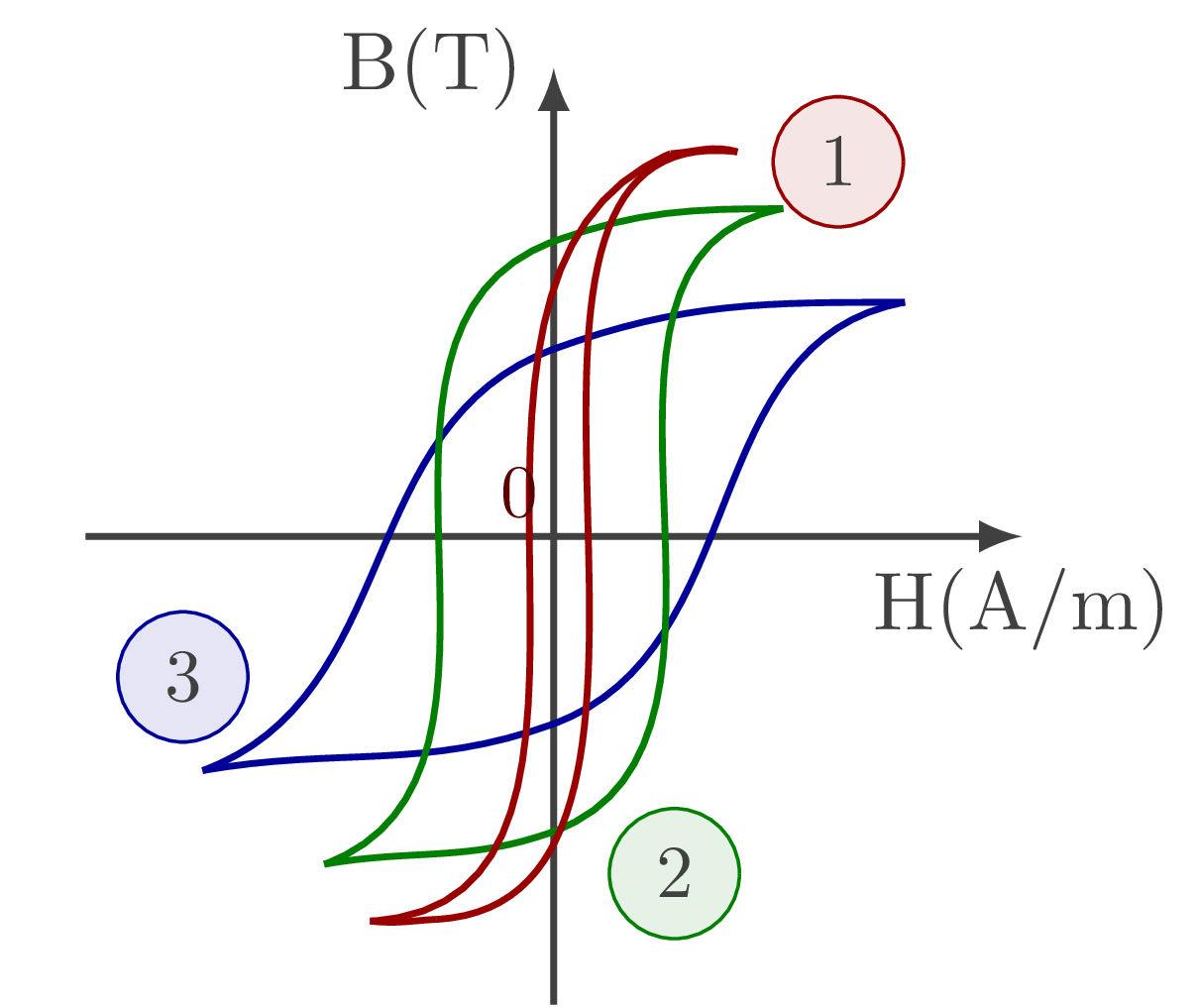
figure-6
Flux d'induction magnétique:
\[\mathsf{\Phi=\vec{B}.\vec{S}}\]
\(\Phi\): le flux de champ magnétique en Webers (Wb);
B: champ magnétique en Tesla (T);
S: surface du circuit plan en mètres carré (m2). \(\vec S\) = \(\vec n\).S
Lorsque le vecteur \(\vec B\) forme un angle \(\alpha\) avec la normale \(\vec n\) à la surface du circuit plan, la formule précédente devient:
\[\mathsf{\Phi=B.S.cos(\alpha)}\]
Pertes dans les matériaux magnétiques:
> Effet de l'hystérésis:
Dans une situation de magnétisation et de démagnétisation, lorsque le matériau doit être re-magnétisé une certaine quantité d'énergie doit être dépensée pour modifier l'orientation des structures élémentaires. Ce changement d'orientation s'accompagne d'une perte d'énergie, par volume de matière, transformée sous forme de chaleur par effet Joule.
Les pertes par hystérésis peuvent être évaluées par la formule:
\[\mathsf{P_h=K_h.f.B_m^{2}}\]
Ph: puissance perdue en Watts par kilogrammes (W/kg);
Kh: coefficient donné;
f: la fréquence en Hertz (Hz);
Bm: champ magnétique en Tesla (T).
> Effet des courants de Foucault:
Lorsqu'un matériau métallique est soumis à un champ magnétique variable, ou s'il se déplace dans un champ fixe, la variation de flux engendre des courants induits circulant dans la masse conductrice, dans un plan perpendiculaire aux lignes d'induction, ce sont les courants de Foucault.
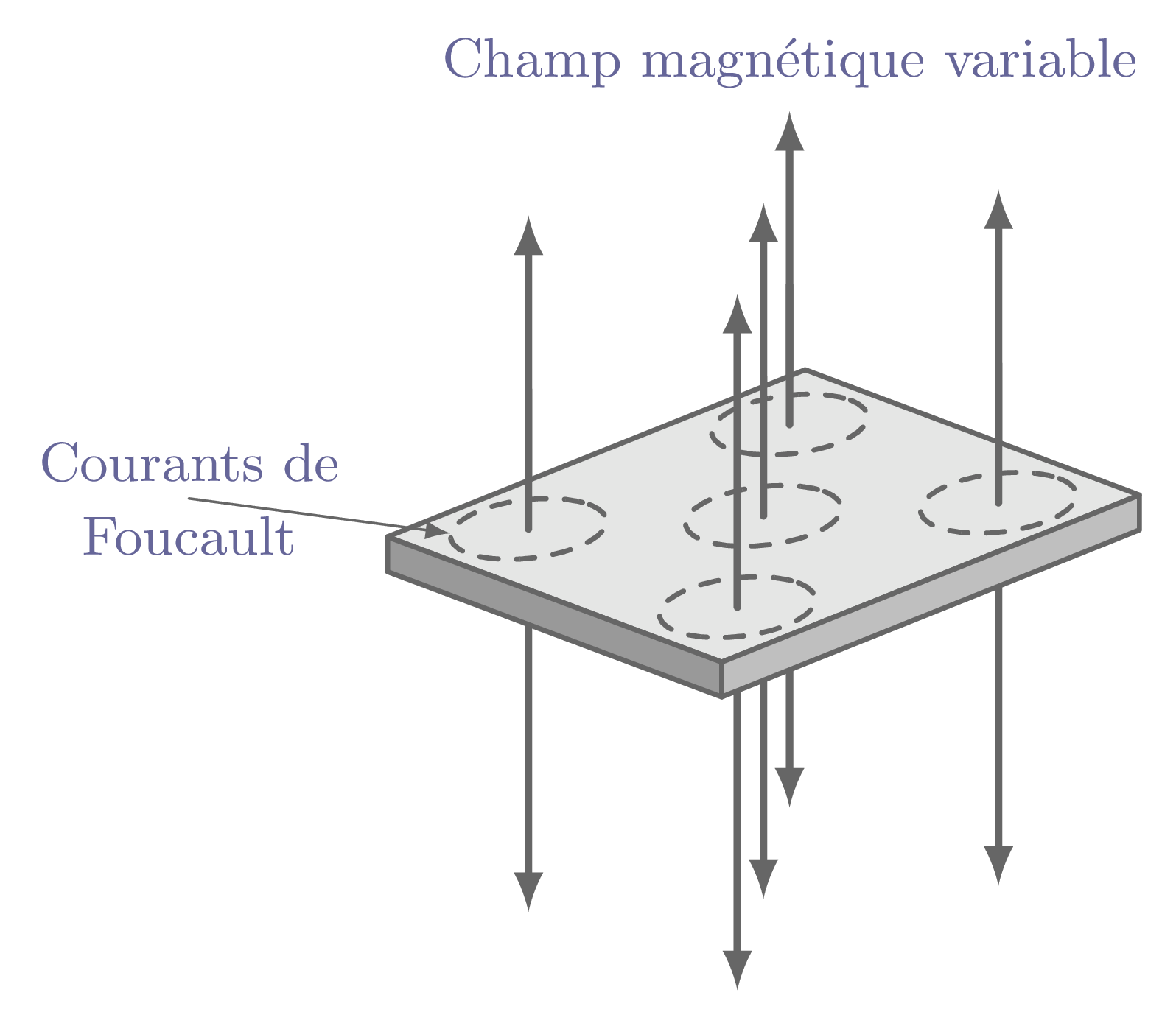
figure-7
Ces courants induits dans les masses conductrices s'opposent à la cause qui leur a donné naissance (d'après la loi de Lenz); cela se traduit par un freinage de la pièce métallique en mouvement. Par exemple, pour le cas du rotor d'un alternateur, l'énergie mécanique qu'il reçoit est absorbée par les forces de freinage et convertie en chaleur par effet Joule dans la masse conductrice. Certaines pièces métalliques (noyau de fer d'électro-aimants, carcasses des transformateurs) soumises à des champ magnétiques variables sont le siège des courants de Foucault engendrant ainsi un échauffement dans leur masse métallique.
Ces pertes sont évaluées par la relation:
\[\mathsf{P_{F}=K_F.\frac{1}{\rho}.e^{2}.B_m^{2}.f^{2}}\]
\(P_{F}\) : la puissance perdue en Watts par kilogrammes de tôle magnétique (W/kg).
\(K_F\) : un coefficient déterminé par mesure sur un échantillon,
\(\rho\) : la résistivité du matériau en Ohm-mètre (\(\Omega\).m)
\(e\) : epaisseur de la masse conductrice en mètre (m)
Bm : induction en Tesla (T).
\(f \): fréquence en Hertz (Hz).
Les pertes engendrées par les courants de Foucault sont à prendre en considération par tous les corps de métiers qui interviennent dans la fabrication des équipements; ainsi:
La fréquence et l'induction étant liées à l'utilisation, les métallurgistes améliorent leurs matériaux en diminuant l'épaisseur e et en augmentant la résistivité.
Les constructeurs réduisent l'intensité des courants de Foucault, en réalisant, non pas une pièce unique, mais un assemblage de pièces métalliques découpées en tranches de faible épaisseur et isolées les unes des autres par une couche de vernis. Le feuilletage est perpendiculaire à la direction des courants de Foucault, bref les lignes de champ doivent être parallèles aux tôles assemblées.
Ceci explique pourquoi les cylindres constituant le rotor et la carcasse des stators des moteurs, des alternateurs, et des transformateurs sont feuilletés.
-> Utilisation:
Bien que les courants de Foucault présentent des inconvénients qu'il faut réduire dans certains situations, ils sont exploités dans d'autres types d'applications; par exemple:
> Les véhicules lourds: le freinage est assuré par des courants induits qui sont développés dans un disque lié à l'arbre en rotation dans l'entrefer d'un électro-aimant. Ainsi, plus la vitesse de l'élément conducteur en mouvement est grande, plus les forces de freinage dues aux courants de Foucault sont élevées.
> Les fours à induction: pour faire fondre certains métaux sensibles à l'action chimique des gaz de combustions, l'énergie électrique due aux courant de Foucault est transformée en chaleur par effet Joule. Les fours à induction sont constitués d'une bobine parcourue par des courants alternatifs de fréquence élevées. Les courants induits de forte intensité se développent dans la masse métallique, provoquant ainsi un dégagement de chaleur.
Grandeurs d'influence :
La variation des caractéristiques d’un matériau magnétique est fonction de:
> La température :
Un matériau ferromagnétique porté à une température supérieur à une certaine valeur appelée point de Curie (par exemple pour le fer pur : 775°C), perd ses qualités magnétiques.
Selon les alliages, cette température est variable ; elle constitue une caractéristique à considérer pour les matériaux portés à haute température.
> Les différents matériaux constituants l’alliage :
Selon les matériaux ajoutés au fer, on obtient des caractéristiques magnétiques différentes.
a) Le silicium : un volume de 1 à 4% de silicium mélangé au fer augmente la perméabilité par rapport au fer pur, la résistivité, ce qui entraîne la diminution des pertes par hystérésis et courants de Foucault.
b) Le carbone : jusqu’à 4% de carbone, l’induction rémanente augmente, le cycle d’hystérésis s’élargit, l’induction de saturation diminue.
c) Aluminium, Nickel : augmentation de la perméabilité, le cycle d’hystérésis est plus étroit.
d) Il existe d’autres éléments qui entraînent aussi des variations de caractéristiques.
> Les pertes fer en Watts par kilogramme :
On résume les pertes par hystérésis et par courants de Foucault par les pertes fer exprimées en Watts par kilogramme de matériau magnétique.
Ordre de grandeur :
Pour des tôles de moteur électrique : 3,6 W/kg
Classification des différents matériaux magnétiques :
Il existe une grande diversité de matériaux magnétiques qui réagissent très différemment selon qu’ils sont soumis à une induction constante ou variable, à partir de ce critère nous établissons la classification suivante:
| Matériaux soumis à induction | Conditions d'emploi | Matériaux types | Utilisation | |
| Induction continue | Permanente: aimants permanents | champ coercitif et induction rémanente élevée pour conserver l'aimantation | Aciers durs, Alliages: fer + aluminium + nickel + cobalt | Tous les aimants: appareils de mesures, volants magnétiques, inducteurs permanents |
| Temporaire: électro-aimants, moteurs à courant continu | Induction maximale pour un champ faible donc µ élevé. Eviter l'aimantation rémanente | Fer pur, acier doux forgé ou moulé | Electro-aimants en courant continu: relais, électro-aimants de contacteurs, pôles inducteurs de machines tournates | |
| Induction alternative | Fréquences 50 - 60Hz: moteurs à courant alternatif | Perméabilité (µ) élevée, pertes faibles par courant de Foucault, cycle d'hystérésis étroit | Tôles d'acier au silicium, Tôles à grains orientés (voir NF C 28 920) | Circuits magnétiques en courant alternatif: moteurs asynchrones, transformateurs,machines synchrones, électro-aimant de conatcteurs |
| Fréquences supérieures à 60Hz: moyennes ou hautes fréquences | Perméabilité importante aux hautes fréquences, faibles pertes par hystérésis et courants de Foucault | Ferrites + cobalt ou manganèse | Circuits magnétiques B.F. et R.F., transformateurs moyenne fréquence, inductances |
tableau-1
Ce tableau (ci-dessus) amène à considérer 4 grandes familles de matériaux magnétiques :
- Les aimants permanents, aimant de portes, alarmes,...
- Les électro-aimants : relais, levage industriel, inducteurs de moteurs,...
- Les circuits magnétiques: pour les fréquences radio, inductances, haut-parleur, écouteurs
- Les circuits magnétiques à fréquences alternatives (50 – 60Hz) transformateurs, moteurs asynchrones.
Analogie électricité - magnétisme:
Terminons cet article par une analogie entre quelques grandeurs électriques et les grandeurs magnétiques:
| Grandeurs électriques | Grandeurs magnétiques | ||
| Intensité du courant | \(I\) | Flux de champ magnétique | \(\Phi\) |
| Densité du courant | \(J\) | Champ magnétique | \(B\) |
| Force électromotrice | \(E\) | Force magnétomotrice | \(F_{mm}\) |
| Résistance | \(R\) | Réluctance | \(R\) |
| Conductivité | \(\gamma\) | Perméabilité | \(\mu\) |
| Conductance | \({1}/{R}\) | Perméance | \({1}/{R}\) |
| Résistivité | \(\rho={1}/{\gamma}\) | Réluctivité | \({1}/{\mu}\) |
tableau-2
Conclusion
Dans cet article, nous avons présenté des notions élémentaires d'électromagnétisme. Mais c'est une spécialité à part entière. Les appareils qui nous entourent au quotidien utilisent en grande partie des matériaux magnétiques. Le terme Pertes fer, employé par les spécialistes désigne les pertes par hystérésis + les pertes dues aux courants de Foucault. La réduction de ces pertes exige le choix de matériaux appropriés.
JtBB

