Les dispositifs numériques permettent de traiter, de stocker et de restituer des informations de façon fiable. En instrumentation, les signaux de mesures des grandeurs physiques sont analogiques. Ce type d’informations doit être traduit sous une forme numérique pour être traité par un ordinateur, un microprocesseur ou un microcontrôleur.
Le convertisseur analogique numérique est un sous-ensemble ou un composant qui transforme un signal analogique (généralement une tension continue fixe ou variable), en une série de valeurs numériques codées. C'est un élément essentiel dans la majorité de dispositifs électroniques modernes. On trouve des convertisseurs analogiques-numériques dans: les ordinateurs, les appareils photos numériques, dans nos précieux smartphones; la belle auto et bien plus encore.
La prise en compte des paramètres techniques des convertisseurs analogiques numériques est déterminante pour choisir le composant le plus adapté à une application.
Ici, nous allons évoquer quatre architectures des convertisseurs analogiques-numériques. En premier nous présenterons des éléments de rappels sur le codage des nombres; ensuite, les caractéristiques générales des convertisseurs analogiques-numériques; les architectures; et pour finir quelques critères de comparaison entre les familles de composants étudiés.
Sommaire
Un peu d'histoire...
Les convertisseurs analogiques numériques voient le jour au début du 20è siècle. Pour améliorer la qualité des transmissions, l'industrie des télécommunications en pleine mutation, se fixe pour objectif de transformer un signal analogique en un signal numérique. Ce sont les transmissions télégraphiques qui en premier, feront usage des convertisseurs analogiques-numériques. La technique de modulation par impulsion et codage (MIC ou PCM) des année 1930, a apporté une amélioration substancielle pour la conception de ces composants. La modulation par impulsion et codage permet de numériser un signal analogique par échantillonnage.
L'invention du circuit intégré, permet la fabrication des convertisseurs analogiques numériques, plus petits et plus rapides. La demande explose dans les années 1970, avec la commercialisation des ordinateurs et les applications audio numériques, avec pour conséquences, la conception et la fabrication des processeurs numériques de signaux (DSP). Dans cette même période, plusieurs architectures de convertisseurs analogiques-numériques sont créées et améliorées.
La famille de convertisseurs analogiques-numériques Sigma-Delta, donne une nouvelle impulsion aux applications audio au milieu des années 1980, transformant ainsi le paysage de l'industrie de la musique.
De nos jours les améliorations sur la vitesse et la résolution de ces composants se poursuivent pour leur utilité dans certaines applications comme l'imagerie médicale, les radars, les télécommunications ou la vidéo.
Codages des nombres
La transformation d’un signal analogique, en une information compréhensible par un système numérique, s’appelle codage ou codification.
Il existe de nombreuses possibilités de codages d’une information : le codage binaire, le codage hexadécimal, le codage ascii, le bcd, …
Codage binaire : il permet de définir une information sous forme d’une série de 1 ou de 0. Ce type de nombre est représenté en base 2.
Codage Hexadécimal : c’est l'écriture d'un nombre en base 16. Avec ce type de codage, l’information est représentée par une combinaison de symboles ayant pour valeurs 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
En notation décimale : l'écriture se fait en base 10, les chiffres qui constituent le nombre peuvent prendre dix valeurs: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Le tableau ci-après montre la correspondance entre ces trois notations:
| Notation décimale | Notation binaire | Notation hexadécimale |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
tableau-1: notations décimale - binaire - hexadécimale
Passage d’un type de codage à un autre
Conversion binaire - décimal
Exemple : convertir en décimal le nombre binaire suivant: 1 1 1 0 1
A l’aide d’un tableau de puissances de 2 :
| 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| - | - | - | - | - | 1 | 1 | 1 | 0 | 1 |
tableau - 2: exemple de conversion binaire - décimal
1 1 1 0 1 = 1×24 + 1×23 + 1×22 + 0×21 + 1×20 = 16 + 8 + 4 + 0 + 1 = 29.
Conversion décimal - binaire
On effectue des divisions successives par deux, puis on prendra tous les restes des divisions en partant du dernier résultat, une autre méthode consiste aussi à utiliser un tableau des puissances de deux.
Exemple : convertir 246 en notation binaire.
Avec des divisions successives par 2, on a:
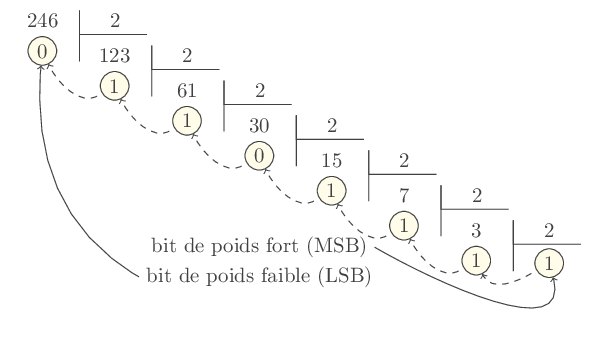
fig - 1: conversion par divisions successives par 2
En partant du dernier résultat, puis du dernier reste, jusqu'au premier (fig-1), on trouve 246 = 1 1 1 1 0 1 1 0
il est possible aussi procéder d'une autre façon, à l'aide d'un tableau des puissances de deux:
| 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
tableau - 3: exemple de conversion décimal - binaire
Par exemple si on reprend le nombre précédent (246) à convertir en binaire :
On constate que : 246 < 256. Donc on fera le calcul 246 – 128 = 118.
128 étant utilisé pour le calcul, on écrit 1 à la 3è ligne du tableau en dessous de 128;
Ensuite le résultat précédent : 118 – 64 = 54
64 étant utilisé pour le calcul, de même on écrit 1 en dessous de 64;
Puis : 54 – 32 = 22
32 étant utilisé, on écrit 1 en dessous de 32;
22 – 16 = 6
16 étant utilisé, on écrit 1 en dessous de 16;
6 < 8, 8 n’est pas utilisé, on écrit 0 en dessous de 8. Et on fait l’opération 6 – 4 = 2, 4 est utilisé, on écrit 1 en dessous de 4.
Puis 2 – 2 = 0, on écrit 1 en dessous de 2;
0 < 1, on écrit 0 en dessous de 1 pour finir. Le tableau ci-dessous illustre le résultat obtenu par cette méthode:
| 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
tableau - 4: résultat de la conversion
246 = 11110110; le résultat est identique.
Conversion binaire - hexadécimal
Exemple: convertir en hexadécimal le nombre binaire 1 1 1 1 0 1 0 1.
Une méthode simple consiste à diviser le nombre binaire de départ en groupe de 4 éléments, puis de faire la conversion:
Selon le tableau-1: 1111 <=> F, et 0101 <=> 5.
1 1 1 1 0 1 0 1 = F5 en hexadécimal (on peut aussi écrire: F5 Hex, ou 0xF5, ou encore F5H).
Conversion hexadécimal - binaire
Exemple: convertir C4 Hex en binaire:
On effectue l'opération inverse. Selon le tableau 1, C correspond à 1100 et 4 à 0100
On a:
C4 Hex = 1 1 0 0 0 1 0 0
Conversion hexadécimal - décimal
Convertir 2BE Hex en décimal, on multiplie les puissances de 16 par les valeurs correspondantes du tableau 1:
2, B et E correspondent respectivement à: 2, 11 et 14.
on a : 2×162 + 11×161 + 14×160 = 702
Conversion décimal - hexadécimal
Exemple: convertir en hexadécimal le nombre 1618.
On procède par divisions successives du nombre par 16, puis on prend les restes des divisions en partant du dernier résultat (comme pour la conversion en binaire).
On trouve 1618 = 652 Hex.
Convertisseur analogique-numérique Présentation
Symbole:
Il existe plusieurs représentations possibles d'un convertisseur analogique-numérique (CAN ou ADC):
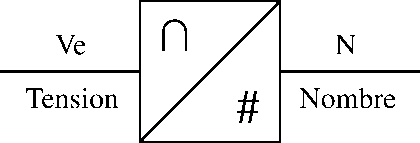
ou
fig-2 images sources: wikibook - fr.wikipedia
Un amplificateur opérationnel, qui fonctionne en comparateur constitue un convertisseur analogique-numérique 1 bit. Il compare une tension à d'entrée par rapport à une tension de référence, puis fournit à sa sortie une valeur binaire 1 ou 0. Ce type de convertisseur est bien entendu inutilisable, de plus il a quelques défauts, notamment son hystérésis, qui peut provoquer des valeurs inattendues en sortie. Mais, l'ampli op fait partie intégrante des architectures que nous présenterons par la suite.
Pour un convertisseur à n bits on pourra aussi utiliser la représentation suivante (fig - 3) :
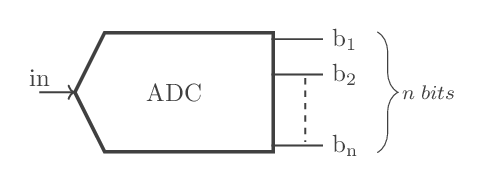
fig-3: autre représentation du CAN
Principe d'une conversion analogique-numérique:
En général, la conversion d'un signal analogique en un signal numérique se fait en trois étapes:
Etape 1: Le conditionnement
C'est la mise en forme du signal à convertir Vin pour qu'il soit présenté à l'entrée du convertisseur (figure xx) :
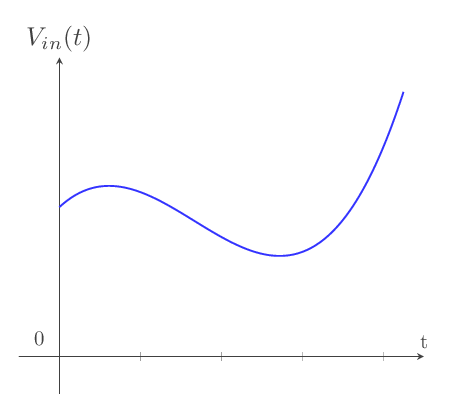
fig-4: conditionnement
Etape 2: L'échantillonnage
Cette opération a pour but de laisser le temps au bloc de traitement logique du convertisseur d'exécuter la tâche qui lui est destinée. Les échantillons du signal d'entrée sont prélevés à des intervalles réguliers
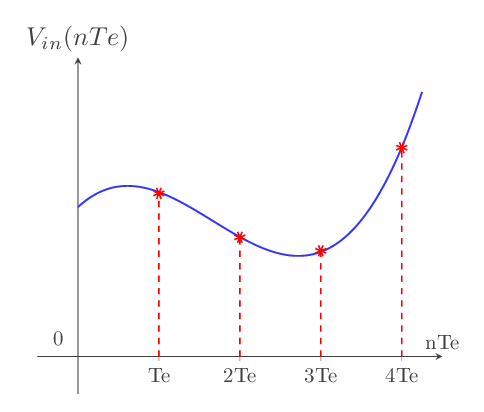fig - 5: échantillonnage
Etape 3 : Le codage
On associe à chaque échantillon un code binaire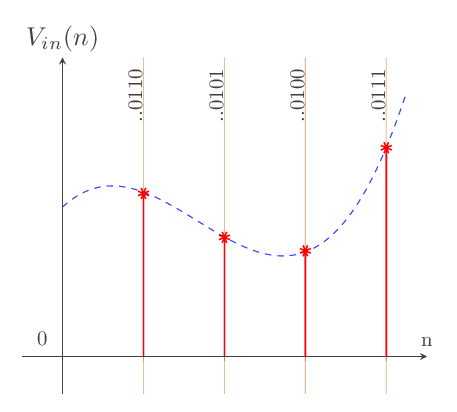
fig - 6: codage
Caractéristiques générales des CAN
Excursion de tension en entrée (Range):
C'est la plage de tension qui peut être lue correctement par le CAN. Elle souvent définie par la tension plein échelle (FSR ou VPE), qui peut être positive ou négative. L'excursion c'est l'écart entre ces deux valeurs (valeur positive du VPE - valeur négative du VPE). Un CAN unipolaire aura une plage d'entrée de 0 à VPE, tantdis qu'un CAN bipolaire aura une palge d'entrée de -VPE à VPE.
Le CAN ne pourra pas délivrer un résultat de conversion fiable si le signal d'entrée est en dehors de cette plage.
Le quantum :
Comme tout composant électronique, le CAN se heurte à des limites pour assurer un fonctionnement idéal.
Le quantum q est une limite due à la quantification. C’est la plus petite variation mesurable entre deux valeurs codées distinctes en sortie.
Il est calculé par:
\[\mathrm{q=\frac{V_{ref}-V_{gnda}}{2^n}}\]
q: quantum en Volts (q = 1 LSB Least Significant Bit);
Vref: tension de référence.
Vgnda: valeur de la tension de masse analogique, certains montages peuvent utiliser une masse virtuelle ayant un certain niveau de tension. Dans la majorité des cas, Vgnda = 0V.
n: nombre de bits du convertisseur.
La tension à convertir Vin (fig - 3) peut se mettre sous la forme :
Vin = q(bn.2n + ...+ b2.21 + b1.20).
Le terme : N = bn.2n+ ... + b2.21 + b1.20 , désigne le mot binaire. La tension Vin peut s’écrire :
Vin = q.N
Caractéristique de transfert d’un CAN :
C’est une représentation graphique du mot binaire N en fonction de la tension d’entrée Vin
Ci-dessous, un exemple de caractéristique d’un CAN 3 bits unipolaire (fig - 8):
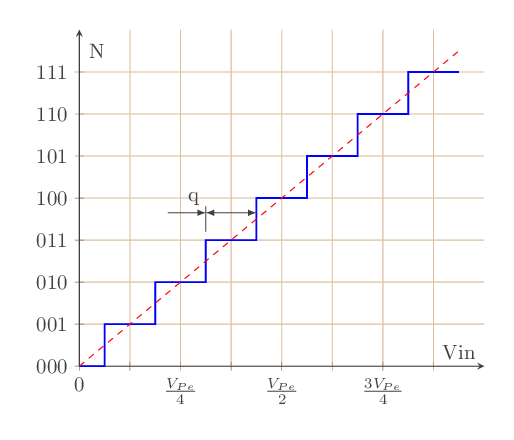fig - 8 : caratéristique de transfert CAN 3 bits
Exemple de caractéristique d’un CAN 3 bits bipolaire (fig - 9)
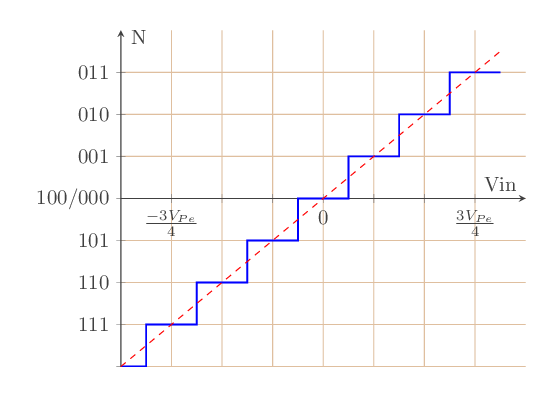fig - 9 : caractéristique de transfert CAN bipôlaire
L’impédance d’entrée :
Elle caractérise la résistance que présente un CAN face à un signal d’entrée. Plus cette valeur est grande, plus la charge vue du signal source est minimale ; cela a pour conséquence de préserver l’intégrité du signal d’entrée.
Quelques caractéristiques métrologiques :
La précision théorique (accuracy) :
Elle caractérise l'écart maximal entre la valeur numérique produite et la valeur de la signal d'entrée correspondant; elle est exprimée en terme de q, rapporté à la pleine échelle. Plus le résultat est petit, plus le convertisseur est précis.
Une haute précision est essentielle dans certaines applications d'instrumentation exigeantes.
La résolution:
C'est la plus petite variation de tension d'entrée que le convertisseur peut détecter. Elle est souvent donnée en nombre de bits. Un CAN avec une résolution de n bits peut représenter le signal d'entrée sur 2n niveaux différents.
Elle est liée l'excursion de la tension plein échelle (valeur positive de VPE - valeur négative de VPE) et au nombre de bits n du convertisseur, et peut être calculée par le rapport (+VPE - (-VPE))/2n.
Pour le cas d'un CAN unipolaire: (-VPE) = 0 , la résolution = VPE/2n.
Pour le cas d'un CAN bipolaire; (-VPE) ≠ 0, la résolution = 2VPE/2n = VPE/(2n - 1).
Le quantum représente la plus petite variation du signal d'entrée que le CAN peut détecter; c'est aussi la résolution du CAN.
La qualité de la représentation du signal dépendra fortement de la résolution. Avec pour conséquence un impact sur les performances. Plus n est élevé, meilleur sera la résolution.
Le temps de conversion:
Tc c'est le temps minimum nécessaire au convertisseur pour stabiliser une donnée en sortie, après que la tension analogique à mesurer lui soit appliquée.
L'erreur de gain:
C'est l'écart entre la caractéristique réelle du CAN et la caractéristique idéale (fig - 10):
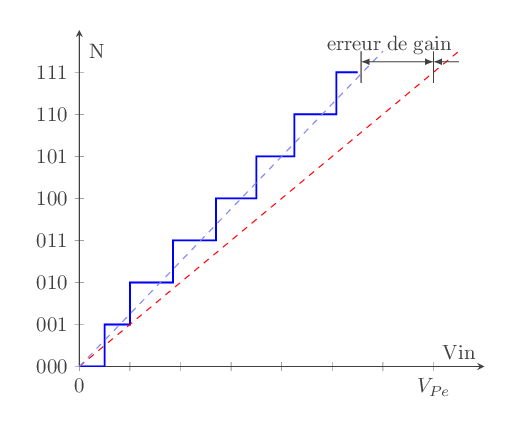fig - 10 : erreur de gain
L'erreur d'offset:
C'est le décalage horizontal de la caractéristique de transfert du CAN
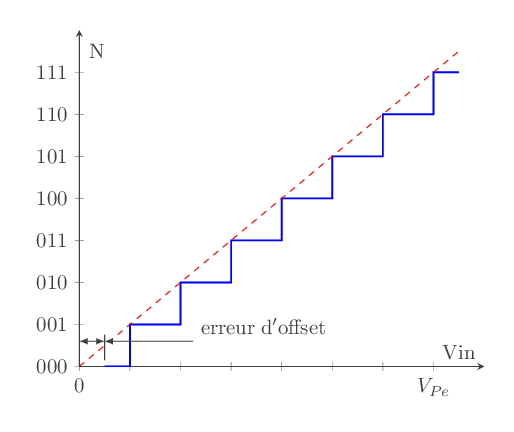fig - 11: erreur d'offset
Dans le cas des appareils de mesure de précision, l'erreur d'offset et l'erreur de gain peuvent fortement entamer la précision. Par exemple pour les instruments biomédicaux, une faible erreur peut entraîner de sérieux dysfonctonnement.
L'erreur d'offset peut aussi avoir un impact sur la tension d'entrée d'un appareil, en décalant sa plage de mesures dynamique, et en la réduisant à une valeur inférieure à la valeur effective. Par exemple une lecture imprécise de la température peut avoir un impact sur le système de gestion d'un procédé.
L'erreur de non linéarité différentielle (DNL) et l'erreur de non linéarité intégrale (INL):
L'erreur de DNL représente le décalage d'un palier de la courbe du CAN:
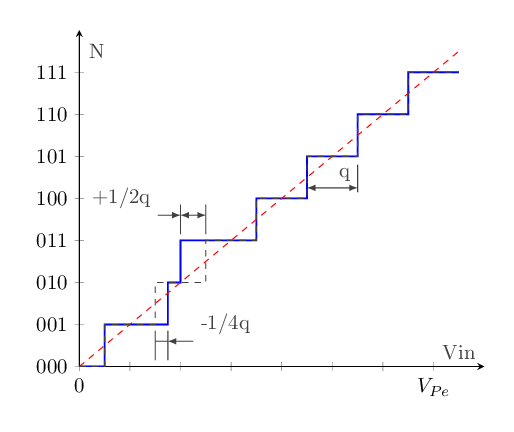
fig - 12: erreur de DNL
L'erreur de linéarité intégrale est une valeur cumulative des erreurs de non linéarité différentielles:
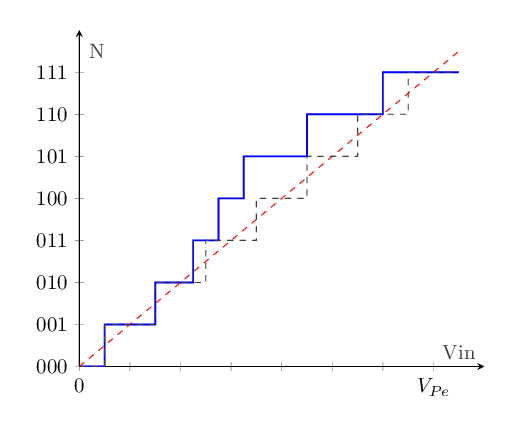fig - 13 : erreur de INL
Les erreurs de DNL et de INL peuvent entraîner la distorsion d'un signal. Pour des applications de traitement d'image ou de l'audio, la qualité des résultats peut être impactée.
Dans le cas d'un système d'acquisition de données, des erreurs de non linéarité peuvent entraîner de mauvais résultats de mesures. Ce type d'erreurs peut être corrigé, au prix d'un système plus complexe.
Erreur de non monotonicité:
En fonctionnement dit normal, une tension d'entrée croissante doit correspondre une énumération croissante des codes en sortie du convertisseur. Si ce n'est pas le cas, on dit qu'il y a non-monotonicité :
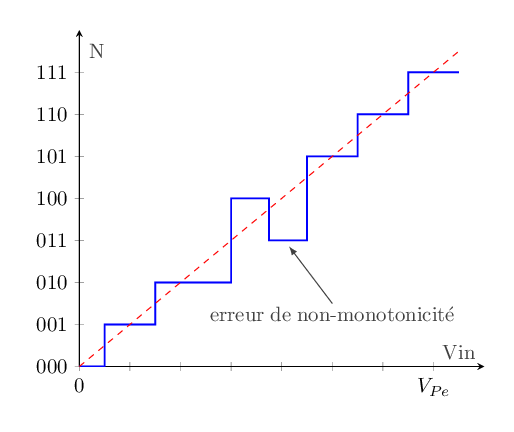
fig - 14 : erreur de non monotonicité
Erreur de quantification:
C'est l'erreur introduite par le processus de quantification :
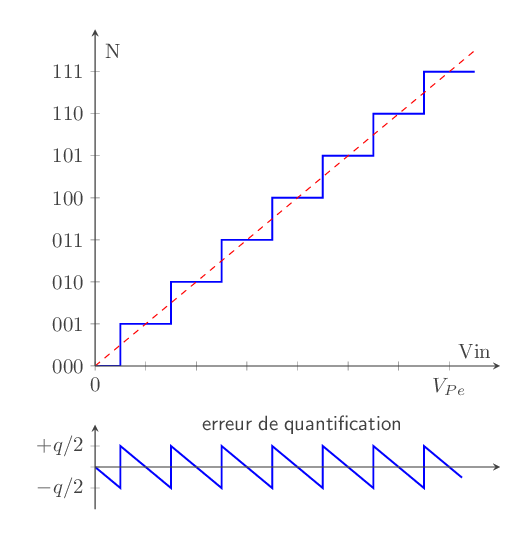fig - 15: erreur de quantification
L'erreur de quantification matérialisée par l'écart entre la valeur analogique vraie de la tension d'entrée Vin et sa représentation numérique.
En général l’erreur de quantification est comprise entre +q/2 et -q/2. Sa valeur est égale à la valeur efficace du signal (fig - 15):
\[\mathrm{\frac{q}{2\sqrt{3}}}\]
Cette erreur est d'autant plus faible que la résolution du CAN est élevée. Dans des applications telles que l'instrumentation bio-médicale ou la musique haute fidélité, où la précision est cruciale, il recommandé d'utiliser des CAN hautes résolutions.
Autres caractéristiques:
Le rappor signal sur bruit (SNR):
Le rapport signal sur bruit (SNR) est le rapport entre la valeur efficace de l'onde sinusoïdale pleine échelle et la somme des bruits aléatoires présents, en supposant que le bruit de quantification est aléatoire et non correlé au signal ou à d'autres bruits.
La "spurious free dynamic range" (SFDR):
Les non-linéarités et les produits d'intermodulation introduisent des harmoniques et des parasites dans le spectre de sortie. La SFDR ou la plage de fréquences dynamiques sans parasites, représente la plage (en dB) entre le fondamental et l'harmonique du parasite le plus élevé, présent dans la plage correspondant à la moitié de la fréquence d'horloge du CAN.
Le rapport Signal distorion par rapport au bruit (SINAD):
C'est le rapport signal sur bruit, mais avec les bruits et les harmoniques du SFDR inclus, considérés comme source de bruits non correlée supplémentaire.
Le nombre de bit effectif en sortie (ENOB):
Il spécifie la dégradation dans la résolution du composant, lors d'une mesure faite quand le CAN introduit le bruit, la distorsion et d'autres type d'erreurs.
Il dépend du SINAD et est estimé par la relation:
\[\mathrm{(ENOB)_{dB}=\frac{SINAD-1,76}{6,02}}\]
Le SINAD étant exprimé en dB de la pleine échelle.
En général, le ENOB est inférieur à la résolution du CAN. Par exemple lorqu'un CAN a ENOB de 8 bits, il est l'équivalent d'un CAN idéal de 8 bits.
La vitesse d'échantillonnage:
Mesurée en échantillons par secondes, la vitesse d'échantillonnage, ou fréquence d'échantillonnage, est un paramètre important du CAN. Elle détermine le nombre de fois que le signal d'entrée est mesuré et converti en valeur numériques, en une seconde.
Exemple d'utilisation du CAN dans les équipements de tests et mesures
La majorité des équipements de tests et mesures modernes reposent sur le bon fonctionnement des CAN, dont le rôle est de convertir le signal analogique issu d’un capteur ou d’une sonde en valeurs numériques qui pourront être traitées, affichées ou analysées.
Parmi les types d’appareils de mesures courants qui existent, on peut citer :
- Les oscilloscopes,
- Les multimètres numériques,
- Les analyseurs de spectres.
Par exemple, prenons le cas d’un oscilloscope :
Celui-ci reçoit un signal d’entrée à travers ses terminaux, via des sondes, en provenance du montage ou du circuit en cours de test.
Un préamplificateur, conditionne le signal reçu, puis l’amplification de ce signal est ajustée par le dispositif de contrôle vertical de l’appareil (par exemple un signal haute tension sera atténué pour que son niveau corresponde à la gamme de mesure).
Le module de gestion de l’axe horizontal de l’oscilloscope se charge de numériser le signal d’entrée à la vitesse d’échantillonnage fixée. La résolution horizontale de l’appareil dépend de ce paramètre.
Le convertisseur analogique numérique convertit le signal en données numériques qui seront affichées sur l'écran à cristaux liquides ou à LED de l’oscilloscope. L’appareil offre ainsi à l’utilisateur les possibilités de stockage, d’analyse et de traitement du signal mesuré. La précision verticale du signal dépend de la résolution du CAN.
Architectures des convertisseurs analogiques-numériques
Parmi de nombreux procédés de conversions analogiques-numériques, il y a:
⦁ Les convertisseurs parallèles;
⦁ Les convertisseurs à approximations successives;
⦁ Les convertisseurs à comptage d'impulsions.
⦁ Les convertisseurs Delta-Sigma.
CAN parallèles ou CAN Flash:
Le principe de ce type de convertisseur consiste à comparer la tension d'entrée Vin à n tensions de références simultanément.
Exemple d’un CAN 3 bits capable de coder 8 valeurs,(fig - 16).
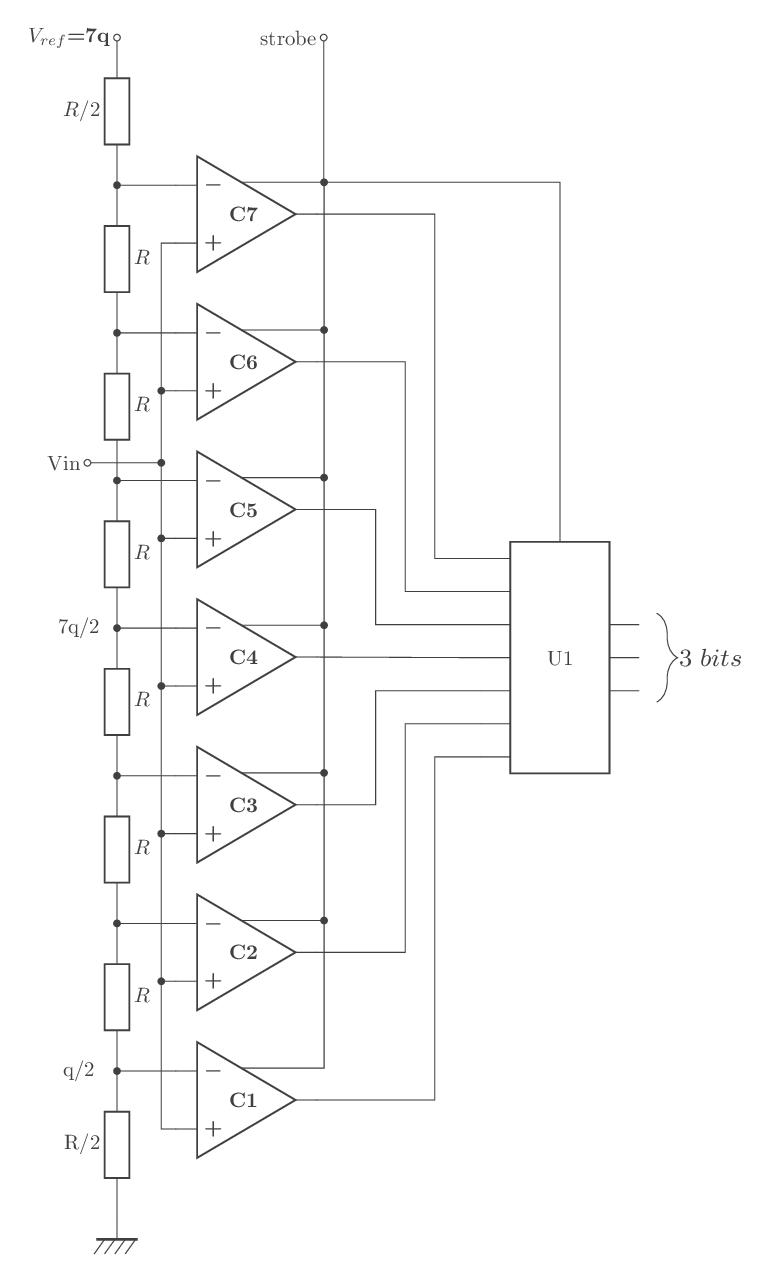
fig - 16: CAN flash 3 bits
Ce montage utilise 7 comparateurs (C1 à C7), un encodeur de priorité 8 vers 3 (U1) et des ponts diviseurs de tension à résistances, dont le rôle est de fixer des valeurs de tensions de références les entrées (-) de chaque comparateur.
On pose:
1LSB = q = Vref/7 (q étant le quantum et Vref la tensionde référence).
Par exemple, supposons que la tension d'entrée Vin = 3V; grâce aux valeurs obtenues par les pont diviseurs de tension à résistances, les sorties des comparateurs C1, C2, C3 passent à 1; tandis que les sorties des autres comparateurs sont à 0. Le circuit U1 récupère et décode toutes ces informations puis délivre en sortie une valeur binaire correspondante à la tension d'entrée 3V.
Les CAN parallèles sont très rapides, car leur durée de conversion n'est limitée que par le temps de propagation à travers les comparateurs et les circuits logiques.
Toute fois pour un convertisseur n bits, il faut 2n - 1 comparateurs.
Ce nombre élevé de comparateurs restreint naturellement le nombre de bits en sortie, et par conséquent la résolution du convertisseur.
Il est possible d’améliorer cette restriction, en créant plusieurs modules de CAN avec un nombre de comparateurs réduits, puis le tout mis en cascade pour n'en former qu'un seul CAN flash: (fig - 17)
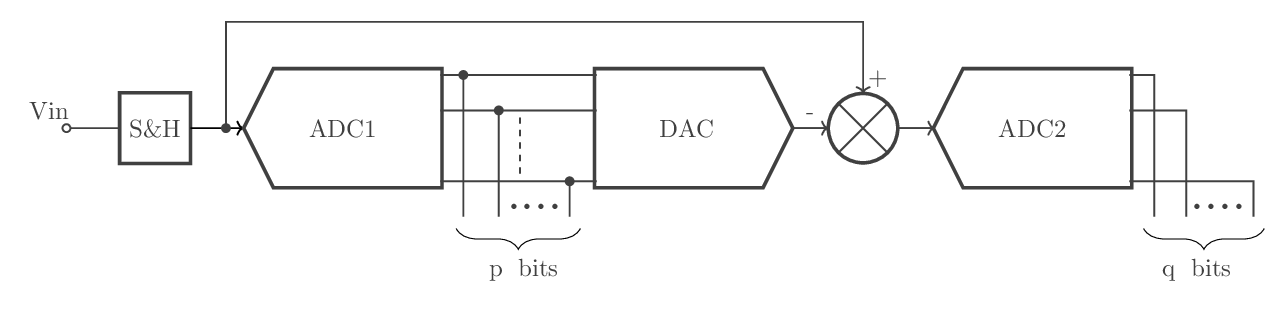
fig - 17: amélioration CAN flash
D’après ce montage (figure xxx), à n bits, un premier CAN (ADC1) , donnera les p bits les plus significatifs ; puis ces p bits sont convertis en valeur analogique V2, grâce à un convertisseur numérique analogique (DAC) placé en aval de ADC1. Si V1 est la tension de sortie de l'échantillonneur-bloqueur (S & H), le second CAN (ADC2) va effectuer la conversion de V1 – V2, pour obtenir les q bits les moins significatifs.
Selon ce principe, le circuit équivaut à un CAN à n bits, avec (n = p + q). L'échantillonneur-bloqueur permet de maintenir la valeur de la tension à convertir pendant toute la durée de la conversion.
Avantages des CAN flash:
Vitesse de conversion rapide; ils ont une conception simple et sont destinés aux applications faible résolution.
Inconvénients:
Le nombre de comparateurs croît de façon exponentielle avec la résolution, cela a pour conséquence une consommation et un coût élevée.
Applications: cette architecture de convertisseur est utilisée par certains oscilloscopes pour capturer des signaux rapides.
CAN à Approximations Successives
Schéma interne simplifié:
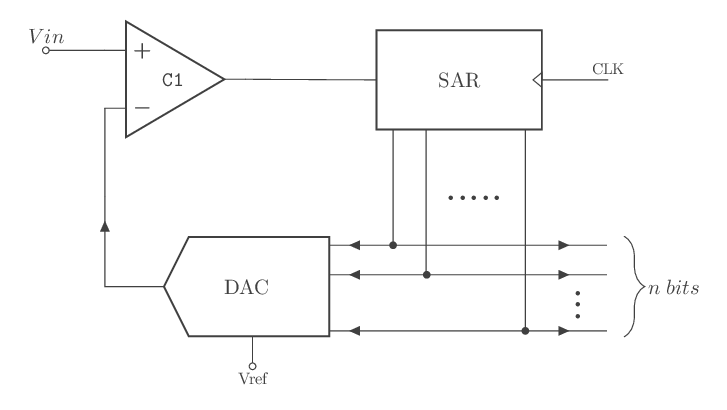
fig - 18: CAN à approximations successives
Le schéma (fig - 18), comprend un comparateur (C1), un registre à approximations successives (SAR), et un convertisseur numérique analogique (DAC).
Principe de fonctionnement:
Au début de la conversion, le registre SAR positionne tous les bits à 0, sauf le bit bn (le MSB ou bit de poids fort). Le CNA (DAC) délivre alors une tension V\(_{DAC}\) égale à Vref/2. Cette tension est ensuite comparée à Vin; si V\(_{DAC}\) est inférieure à Vin, la valeur binaire du MSB reste à 1, ensuite le registre SAR positionne à 1 le bit de poids inférieur; si V\(_{DAC}\) devient supérieure à Vin, le registre positionne à 0 ce bit, passe à la sortie binaire immédiatement inférieure la positionne à 1, puis une nouvelle comparaison est effectuée; ce cycle se poursuit jusqu’au bit de poids faible (LSB). La valeur binaire à la fin de la conversion sera proche ainsi de celle de la tension d’entrée.
Le graphe ci-après (fig - 19) illustre une représentation graphique de la tension de sortie du convertisseur numérique analogique en prenant en exemple un CAN 3 bits:
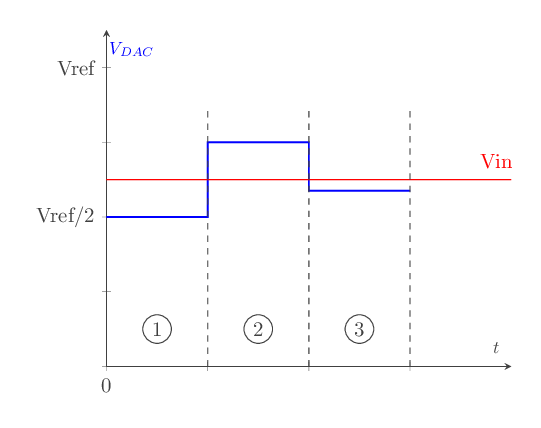
fig - 19: sortie CNA pour un CAN 3 bits
La tension de référence = 5V. On suppose que la tension à convertir vaut 3V par exemple.
La conversion démarre avec la Phase 1:
Phase 1: le régistre à approximations successive positionne uniquement le bit de poids fort à 1. La sortie du convertisseur numérique analogique délivre une tension de 2,5V. La tension d'entrée Vin = 3V > 2,5V; le bit de poids fort est maintenu à 1.
Phase 2: le régistre positionne à 1 le bit immédiatement inférieur, la tension de sortie du convertisseur numérique analogique devient supérieure à la tension d'entrée Vin = 3V. Le régistre positionne ce bit à 0, puis poursuit son cycle à la phase 3.
Phase 3: C'est au tour du bit de poids faible d'être mis à 1. La tension de sortie du convertisseur numérique analogique est légèrement en dessous de Vin = 3V. Ce bit est maintenu à 1.
Puis le cycle s'arrête, puisque le bit de poids faible est atteint. La valeur numérique de la tension d'entrée affichée par le régistre (SAR) est égale à 101 en binaire.
Il est souvent indispensable d’associer un CAN à Approximations successives à un échantillonneur bloqueur, l'ensemble étant piloté par des signaux spécifiques d'horloge. L'utilisation de l'échantillonneur entraîne aussi la présence d'un filtre (fig-20):
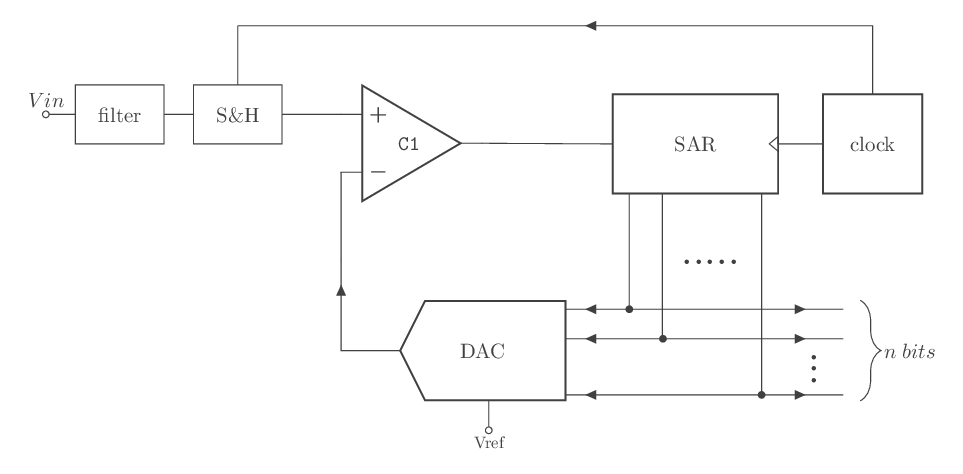
fig - 20: amélioration d'un CAN à approximations successives
Avantages des convertisseurs à approxamtion successives:
Faible consommation, durée de conversion de l'ordre de quelques dizaines de micro-secondes. Même si cette durée est plus élevée que celle des convertisseurs flash, le compromis "complexité-vitesse" les rends avantageux vis à vis de ces derniers.
Inconvénients
Les CAN à approximation successives ne sont pas appropriés pour des applications hautes vitesses. La temps de conversion Tc est variable, car il dépend de la tension d'entrée Vin.
Applications: ce type de convertisseur peut être utilisé dans des systèmes d'acquisition de données ou des système à autonomie d'énergie, datalogger portable.
Convertisseurs à comptage d'impulsions:
Ce type de convertisseur nécessite peu de composants mais offre une très bonne précision. Toutefois le temps de conversion est considérablement plus long que celui des deux familles précédentes.
Les CAN à comptage d’impulsions les plus répandus sont :
⦁ Les convertisseurs simple rampe ;
⦁ Les convertisseurs double rampe ;
⦁ Les convertisseurs triple rampe ;
⦁ Les convertisseurs quadruple rampe ;
⦁ Les convertisseurs Tension - Fréquence.
Convertisseur analogique-numérique simple rampe:
Le principe consiste à comparer une rampe de tension, à la tension à mesurer Vin par rapport à une tension nulle. L’intervalle de temps t1 – t0, qui représente dans ce cas la durée de cette comparaison, est proportionnel à Vin.
Le nombre d’impulsions délivrées par une horloge et comptées pendant cet intervalle de temps est fonction de Vin.
Un exemple de montage valable uniquement pour Vin >0, est donné par la figure suivante (fig - 21):
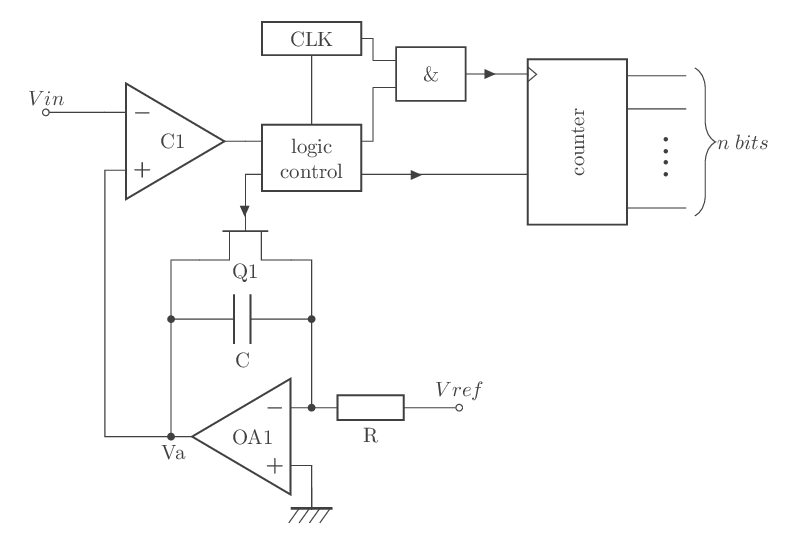fig - 21 : convertisseur analogique numérique simple rampe
Principe: (graphique fig - 22)
Supposons qu’on veut convertir une tension Vin > 0.
La rampe de tension Va fournie par l’intégrateur est comparée directement à Vin. Cette rampe est générée au moment du déclenchement de la mesure, à l’instant t = t0 ; Va est inférieure à Vin, la sortie du comparateur (C1) est égale à zéro ; l’entrée de "comptage" est active, le compteur incrémente ses valeurs numériques en sortie au rythme des impulsions présents sur son entrée d'horloge.
Lorsque Va atteint le niveau de Vin, la sortie du comparateur passe à 1. L’entrée "comptage" devient inactive et le compteur s’arrête. A t = t1, le transistor à effet champ conduit et décharge le condensateur à travers sa résistance à l'état passant (RDSon).
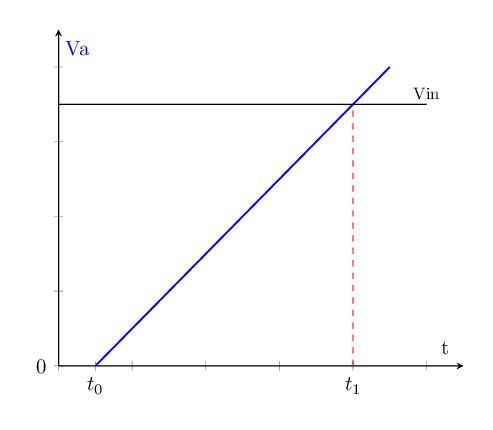fig - 22: sortie de l'intégrateur CAN simple rampe
Le nombre d’impulsions d'horloge N de période T compté, pendant l’intervalle de temps t1 – t0, est proportionnel à Vin
La tension d'entrée Vin n'est pas toujours positive, mais peut être de polarité quelconque (positive ou négative). Le montage (fig - 21) n'est plus valable dans ce cas.
Convertisseur analogique-numérique double - rampe
Le schéma bloc (fig - 23) ci-après illustre son fonctionnement
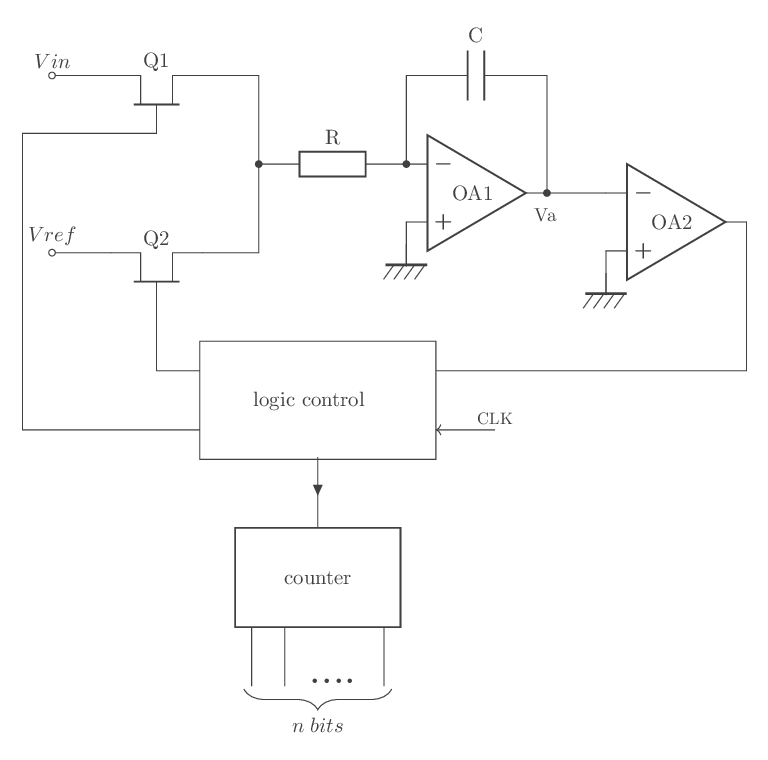
fig - 23 : CAN double rampe
Au départ à l’instant t0, la tension Vin à convertir est appliquée à l’entrée du générateur de rampe ; grâce à la logique de commande. Le générateur de rampe intègre cette tension pendant un intervalle de temps t1 - t0, un compteur mesure cet intervalle de temps, soit N1 périodes T d’horloge (première rampe).
On obtient :
\[\mathrm{\frac{1}{RC}\int_0^{t_1}Vin.dt=\frac{Vin}{RC}t_1=\frac{Vin}{RC}N_1T}\]
Ensuite la logique de commande commute la tension de référence Vref de polarité opposée à Vin, sur l’entrée de l’intégrateur.
La tension de sortie de l’intégrateur décroît linéairement selon une pente constante, jusqu’à l'instant t2 (deuxième rampe) ; le compteur compte la durée de cette décroissance, soit N périodes T d’horloge.
On obtient :
\[\mathrm{\frac{Vref}{RC}NT}\]
On peut alors écrire
\[\mathrm{\frac{Vin}{RC}N_1T=\frac{Vref}{RC}NT}\]
Ce qui donne au final:
\[\mathrm{Vin= \frac{Vref}{N_1}N}\]
Le graphique ci-après (fig - 24) montre ce fonctionnement
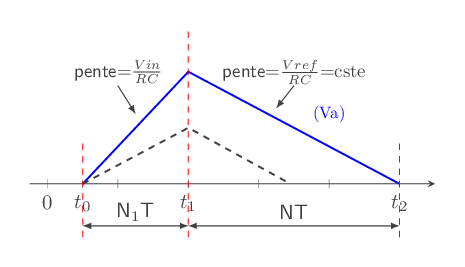
fig - 24 : fonctionnement CAN double rampe
Avantages du convertisseur double rampe: bonne précision, bonne résolution, l'instabilité à long terme n'a pas d'influence sur la mesure.
Inconvénients:
> Temps de conversion élevé
> La non linéarité de la rampe d’intégration, peut aussi être une source d'erreur possible.
> La présence d'une des résistances RDSon des transistors à effet champ à l'état passant dans le montage. Cette résistance s’ajoute à la résistance R de l’intégrateur. De plus elle peut-être sujette à des variations de température ; ce qui peut entraîner des erreurs de fidélité dans le cas d’utilisation dans un appareil de mesure.
> L’intégrateur à amplificateur opérationnel est sujet à des tensions de décalage, pouvant entraîner des erreurs.
Par exemple supposons une tension de décalage de quelques centaines de µV/°C ; pour un voltmètre de 20000 points avec Vref = 5 V, la sensibilité sera de :
5 / 20000 = 250 µV.
Une variation de température de quelques degrés sera donc suffisante pour affecter le bit de poids faible de l’appareil.
Applications:
Bien que le temps de conversion soit assez long en rapport aux convertisseurs flash et par approximations successives, en tenant compre de ses avantages, ce type de composants est utilisé par les dispositifs électroniques des multimètres numériques.
Convertisseur analogique-numérique triple - rampe:
Pour ce type de convertisseurs, la première étape du convertisseur double rampe est conservée. L’étape qui suit comporte deux phases :
Phase 1 : une décharge très rapide du condensateur à partir de l’instant t = t1, jusqu’à une tension de seuil Vs très faible. Pour obtenir cette décharge rapide, la résistance R de l’intégrateur est substituée par une résistance R’, 100 fois plus petite que R.
Soit N2, le nombre d’impulsions d’horloge comptées pendant cette décharge ; lorsque la tension d’entrée Vin = V, on peut écrire :
\[\mathrm{V = Vs + \frac{Vref·100·N_2·T}{RC}}\]
Phase 2 : dans cette courte phase, un détecteur de Vs placé à la sortie de l’intégrateur subtitue de nouveau R’ par R (le résistance de départ) lorsque sa tension de sortie atteint Vs.
Soit N3 le nombre d’impulsions d’horloge comptée durant cette phase, dont le comptage s’arrête lorsque Va = 0 ; on a dans ce cas :
\[\mathrm{Vs=\frac{Vref·N_3·T}{RC}}\]
Le bilan de la première étape et des deux phases de l’étape suivante donnera :
\[\mathrm{\frac{Vin}{RC}N_1T=\frac{Vref}{RC}·100N_2T+\frac{Vref}{RC}N_3T}\]
\[\mathrm{Vin=\frac{Vref}{N_1}(100N_2+N_3)}\]
La décharge du condensateur peut être ralentie dans la deuxième phase pour permettre un comptage précis des dernières impulsions.
Le graphique ci-dessous illustre ce fonctionnement :
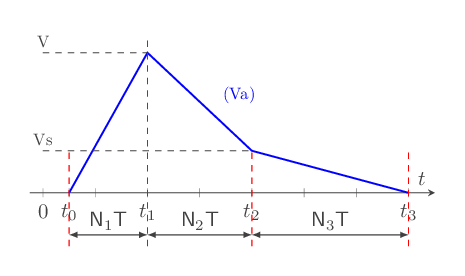fig - 25: fonctionnement CAN triple rampe
Convertisseur analogique-numérique quadruple - rampe:
De façon sommaire, on peut dire qu’un convertisseur analogique numérique double rampe auquel on ajoute deux phases supplémentaires pour compenser les erreurs de décalage, est un convertisseur quadruple rampe.
L’intégrateur d’un CAN quadruple rampe présente quatre modes de connexion:
> Une capacité C court-circuitée en dehors de la durée de conversion,
> Une entrée mise à la masse,
> Une tension de référence appliquée à l’entrée,
> La tension d’entrée à convertir Vin appliquée à l’entrée.
L’entrée (+) de l’intégrateur se trouve en permanence au potentiel Vref/2.
Convertisseur Tension – Fréquence
Les convertisseurs simple rampe sont sensibles aux bruits. Ces derniers peuvent être éliminés par des filtres. Une alternative à cette solution consiste à superposer les bruits périodiques au signal utile, en appliquant ce signal à l’entrée de l’intégrateur ; d’où l’intérêt d’un convertisseur tension – fréquence.
Le convertisseur tension – fréquence convertit une tension d’entrée Vin en un signal périodique dont la fréquence f est proportionnelle à Vin.
La mesure de la fréquence f se fait en comptant le nombre d’impulsions d’horloge dans un intervalle de temps.
Principe (fig - 26):
Une tension Vin appliquée à l’entrée de l’intégrateur génère une rampe. Lorsque la rampe atteint la tension de référence Vref, le comparateur bascule, puis un monostable génère une impulsion qui va commander la décharge rapide du condensateur. Par le fait de la présence d'un générateur de courant de précision, le courant continue de circuler à travers le condensateur; la vitesse des impulsions générées par le monostable est proportionnelle à la vitesse de charge de l'intégrateur et par conséquent à la tension Vin.
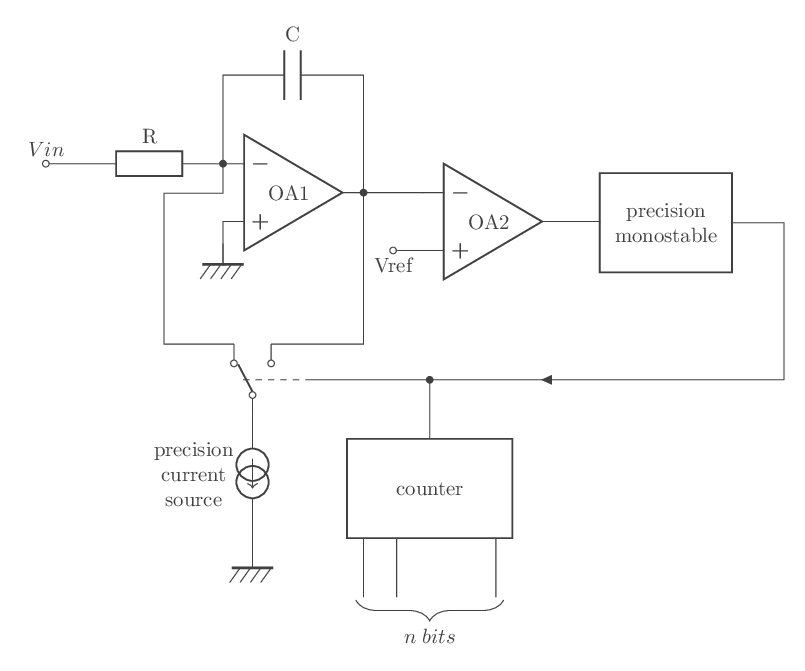fig - 26: convertisseur tension-fréquence
L'emploi d'un générateur de courant, pour décharger le condensateur, permet la conservation de la charge, lorsque le comparateur bascule. Ce montage est dit à équilibrage de charge.
Si ce composant est conçu pour résister aux signaux parasites, sa précision cependant reste liée à la précision et à la stabilité de : l’intégrateur, l’horloge et la tension de référence.
Convertisseur analogique-numérique Sigma-Delta
Pour comprendre son fonctionnement, il faudra d'abord remonter aux phases de développement des technologies télécoms où la modulation par impulsion et codage (MIC ou PCM), était mise en oeuvre, dans le but d'améliorer l'efficacité des transmissions.
Le convertisseur analogique-numérique Sigma-Delta, est assez particulier. Il est composé d'une fraction d'électronique analogique, et d'une autre fraction d'électronique numérique. Présenter de façon détaillée ce composant ici pourrait nous conduire vers d'autres points de vue techniques comme: le suréchantionnage, le filtrage numérique, la mise en forme du bruit,...Cela nous éloignera du cadre fixé dans ces quelques lignes.
De façon sommaire, nous pouvons dire que, le convertisseur analogique-numérique Sigma-Delta est composé de deux modules principaux (fig - 27):
- Le modulateur Sigma-Delta, schématisé par le système bouclé formé d'un différentiateur (OA1), d'un intégrateur (OA2), d'un comparateur (C1) et d'un convertisseur numérique analogique (DAC) sur 1 bit. Le signal d'erreur issu du différentiateur est intégré puis soumis à un comparateur qui pourra délivrer un flot de données sur 1 bit. Pour résumer, le modulateur Sigma-Delta à pour rôle de convertir le signal analogique d'entrée en un flot de données numériques sur 1 bit; en utilisant la technique du suréchantillonnage et de "mise en forme" du bruit.
- Le filtre numérique en sortie du modulateur Sigma-Delta, constitue la dernière étape de la fonction recherchée. Il filtre le flot de données en sortie du comparateur et le traduit en information numérique haute résolution codée sur N bits.
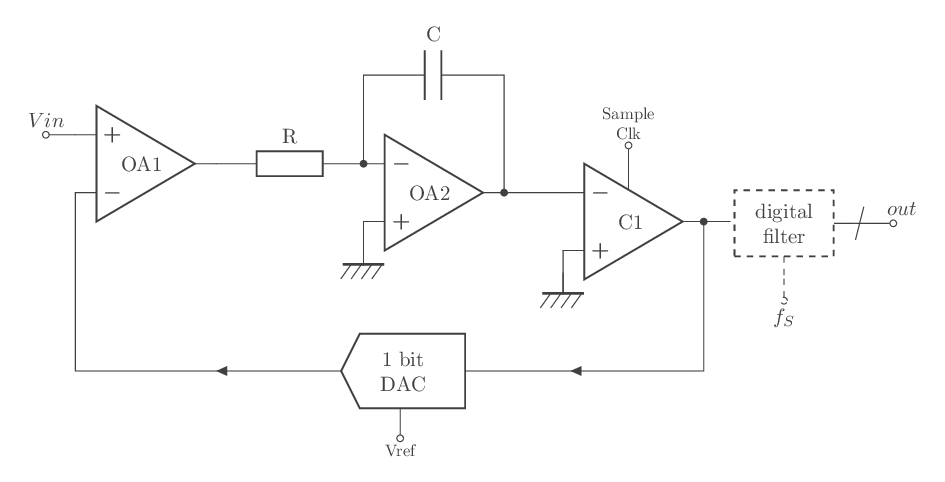
fig - 27: convertisseur sigma delta
Utilisations possibles : l’audio, l’instrumentation de mesure de précision, les appareils où les performances face au bruit sont critiques, mesure de température, thermocouples.
Exemple d'application: mesure de la consommation d'un moteur à courant alternatif à l'aide d'une résistance shunt.
Avantages: plus fiable que les composants analogiques; très haute résolution avec un ENOB de 20 - 24 bits; ils ont une précision accrue grâce à l'emploi de filtres numériques.
Inconvénient: faible vitesse d'échantillonnage.
Pour mieux comprendre le fonctionnement de ce composant, le constructeur Analog Devices, propose dans site un simulateur à cet effet (Voir ref [2]).
Quelques critères de comparaison
Le tableau ci-après établit la comparaison sur quatre architectures de convertisseurs analogiques-numériques, en tenant compte de quelques critères parmi tant d'autres; à savoir: la résolution, la vitesse, la consommation, les performance par rapport au bruit, et le type d'applications possibles.
| Type de CAN | Résolution | Vitesse | Consommation | Performance/bruit | Application typique |
| Flash | Basse à moyenne | élevée | élevée | basse | Acquisition de données, radar |
| Approximation successives | Moyenne à grande | moyenne | élevée | modérée | Acquisition de données, appareil d'usage générale. |
| Comptage d'impulsions (double rampe) | haute | basse | basse | haute | Mesure de précision, multimètres. |
| Sigma Delta | haute | basse à moyenne | moyenne | haute | Audio, instrumentation. |
tableau - 5: comparaison des CAN
Conclusion
Un convertisseur analogique-numérique (CAN) est un composant clé dans un système électronique numérique moderne, dont Il assure l'interface avec les composants analogiques (capteurs ou sondes de mesure, ...). Les convertisseurs analogiques-numériques sont présents dans les technologies IoT, l'insdustrie automobile, l'instrumentation bio-médicale, les technologies de l'intelligeance artificielle et du machine learning. De nombreuses familles de microcontrôleurs embarquent des CAN; toute fois pour des applications à haute résolution, l'emploi d'un composant externe sera nécessaire. Dans cet article, nous avons présenté quelques types de convertisseurs, mais le marché regorge de technologies diverses. Pour aller plus loin les constructeurs proposent dans leur sites, des mines d'informations sous forme de notes d'applications expliquant en détail le fonctionnement de ces composants.
Eléments bibliographiques:
[1] Converters - Chap.6 - sec. 6 - 2 Analog-to-dgital converter - Architectures Analog Devices - (site de analog devices).
Liens internet:
[2] https://www.analog.com/en/resources/interactive-design-tools/sigma-delta-adc-tutorial.html
[3] https://www.keysight.com (oscilloscopes)
[5] https://commons.wikimedia.org
[6] https://fr.wikipedia.org/wiki/Fichier (image Symbole_CAN)
JtBB
