Signal périodique:
Un signal est dit périodique lorsqu'il se répète de façon identique après le même intervalle de temps.
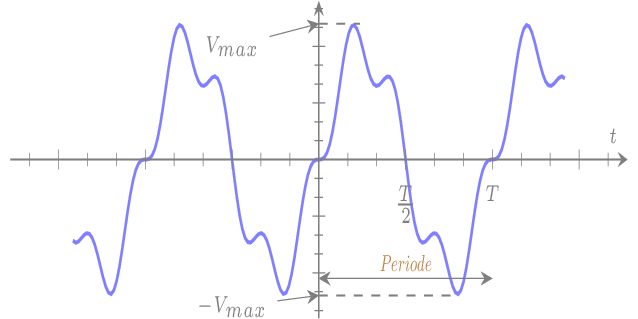
Sa période T en secondes, est l'ntervalle de temps, où il se répète à l'identique.
La fréquence d'un signal c'est le nombre de fois que le signal se reproduit à l'identique toutes les secondes.
\[\bbox[5px,border:1px solid]{\mathsf{F=\frac{1}{T}}}\]
F en Hz et T en s
La pulsation \(\mathsf{ω = 2πF =\large{\frac{2π}{T}}}\); ω en rd/s (radian par secondes).
Le signal évolue de -Vmax à Vmax. Son amplitude est égale à Vmax -(-Vmax) = 2Vmax.
Notion de valeur moyenne:
Exemple: un sachet contient des écrous de diamètres différents.
| nombre d'écrous | diamètre (mm) | |
| écrou de type 1 | 3 | 10 |
| écrou de type 2 | 1 | 8 |
| écrou de type 3 | 4 | 12 |
| écrou de type 4 | 2 | 14 |
Pour calculer le diamètre moyen m des écrous, on fera l'opération:
Par analogie avec l'exemple précédent, si on a un signal périodique V(t), la valeur moyenne égale à la somme de toutes les valeurs instantanées sur une période divisée par la période.
La valeur moyenne d'un signal périodique = \(\large{\frac{\text{l'aire du signal sur une période}}{\text{période}}}\).
Autrement ce sera = \(\large{\frac{\text{l'aire de la partie positive − aire de la partie négative}}{\text{la période}}}\), s'il s'agit d'un signal qui change de signe au cours du temps.
En notation mathématique l'aire est définie par:
\[\mathsf{aire = \int_{0}^{T}V(t)dt}\]
Pour un signal périodique V(t) de période T, la valeur moyenne:
\[\bbox[5px,border:1px solid]{\mathsf{\overline{V}=\large{\frac{1}{T}\int_{0}^{T}V(t)dt}}}\tag{1}\label{1}\]
Exemple 1:
Le signal V(t) est sinusoïdal: V(t) = Vmax sin(ωt);
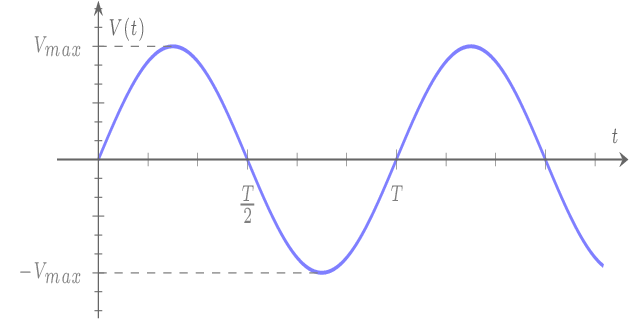
La valeur moyenne est = \(\large{\frac{\text{Aire du signal sur la période T}} {T}}\); comme le signal change de signe durant sa période, la valeur moyenne =
L'aire de la partie positive = l'aire de la partie négative; donc cette valeur moyenne est nulle.
Mesure de la valeur moyenne:
Pour mesurer la valeur moyenne du signal avec le multimètre, il faut mettre l'appareil en position DC.
Notion de valeur efficace:
Une résistance traversée par un courant électrique, va dissper la puissance qu'elle consomme sous forme de chaleur. On le constate avec notre cafétière dès sa mise en marche, c'est aussi le cas d'un radiateur électrique de chauffage par exemple.
On calcule cette puissance avec la loi d'Ohm:
\[\mathsf{P=RI^2};\]
\[\text{P en Watts (W), R en Ohms (Ω) et I en Ampères (A)}\]
Le courant distribué par le fournisseur d'électricité est alternatif, c'est à dire qu'il change alternativement de sens. Ce courant a la même allure que la tension sinoïdale V(t) en exemple 1.
Si on fait passer ce courant à travers la résistance, sa valeur moyenne peut être calculée grâce à la formule:
\[\mathsf{\overline{I} = \frac{1}{T}\int_{0}^{T}i(t)dt}\]
Mais \(\overline{I}\) = 0, puisque l'aire de la partie positive du signal est égale à celle de la partie négative.
Si à présent on calcule la puissance: \(P=R\overline{I}^2 = 0\). Ce calcul porte à croire que la puissance consommée par la résistance est nulle, mais c'est tout de même bizzare puisqu'elle chauffe sans tenir compte des changements de sens (ou de signe) du courant électrique.
Donc la puissance est bien différente de 0. C'est pour cette raison qu'on définit la notion de courant efficace pour appliquer les lois de puissances en régime alternatif.
Le courant efficace est donné par la formule mathématique suivante:
\[\mathsf{[i_{eff}]^2 = \frac{1}{T}\int_{0}^{T}i(t)^2dt}\]
On peut donc dire que pour un signal périodique V(t) de période T, la valeur efficace notée VRMS sera:
\[\mathsf{V_{RMS}^2=\frac{1}{T}\large{\int_{0}^{T}V(t)^2dt}}\]
Soit:
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=\sqrt{\frac{1}{T}\large{\int_{0}^{T}V(t)^2dt}}}}\tag{2}\label{2}\]
Mesure de la valeur efficace:
Pour mesurer la valeur efficace d'un signal, il faut mettre le multimètre en position AC. Toute fois dans ce mode l'appareil va redresser le signal puis mesurer la valeur efficace de l'ondulation du signal (RMS).
Mais pour une mesure précise, il faudrait placer le multimètre (si la fonction existe) en position AC+DC; dans ce mode, l'appareil effectue le calcul \(\mathsf{\sqrt{\frac{1}{T}\int_{0}^{T}[V(t)]^2dt}}\), puis affiche la valeur efficace vraie (TRMS). Un grand nombre d'appareils du commerce possèdent cette fonction.
Exemples de calculs:
On va se limiter ici au calcul de la valeur moyenne et efficace de quelques signaux périodiques.
Signal sinusoïdal:
Si V(t) est un signal sinusoïdal d'amplitude Vmax et de période T:
V(t) = Vmax sin(ωt).
L'allure de V(t) est identique à celle de l'exemple 1.
Valeur moyenne de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{\overline{V}=0}}\]
Cela a été démontré dans l'exemple 1
\[\mathsf{\overline{V} =\frac{1}{T}\int_{0}^{T}V(t)dt=\frac{1}{T}\int_{0}^{T}V_{max}sin(ωt)dt\;\;(\text{avec}\; ω=\frac{2π}{T})}\]
\[\mathsf{=\frac{1}{T}\int_{0}^{T/2}V_{max}sin(ωt)dt - \frac{1}{T}\int_{T/2}^{T}-V_{max}sin(ωt)dt}\]
\[\mathsf{=\frac{V_{max}}{ωT}\left(\left[-cos(ωt)\right]_{0}^{T/2} + \left[-cos(ωt)\right]_{T/2}^{T}\right)}\]
\[\mathsf{=\frac{V_{max}}{ωT}\left(2-2\right)=0}\]
Valeur efficace de V(t):
D'après la formule (2),
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=\frac{V_{max}}{\sqrt{2}}}}\]
On peut retrouver ce résultat par calcul
\[\mathsf{V_{RMS}^2=\frac{1}{T}\large{\int_{0}^{T}V(t)^2dt}}\]
\[\mathsf{=\frac{1}{T}\int_{0}^{T}[V_{max}sin(ωt)]^2dt}\]
On pose ωt = θ; lorsque t varie de 0 à T, θ varie de 0 à 2π
\[\mathsf{=\frac{1}{2π}\int_{0}^{2π}V_{max}^2sin^2θdθ}\]
\[\mathsf{=\frac{1}{2π}\int_{0}^{π}V_{max}^2sin^2θdθ+\frac{1}{2π}\int_{π}^{2π}V_{max}^2sin^2θdθ}\]
La primitive de \(\mathsf{sin^2(θ)=\frac{1}{2}\left(θ-\frac{1}{2}sin(2θ)\right)}\);
\[\mathsf{=\frac{V_{max}^2}{2π}\left(\left[\frac{1}{2}\left(θ - \frac{1}{2}sin(2θ) \right)\right]_{0}^{π}+\left[\frac{1}{2}\left(θ - \frac{1}{2}sin(2θ) \right)\right]_{π}^{2π}\right)}\]
\[\mathsf{=\frac{V_{max}^2}{2\pi}\left(\frac{π}{2}+\frac{π}{2}\right)}\]
\[\mathsf{=\frac{V_{max}^2}{2}}\]
\[\text{donc }\mathsf{V_{RMS}=\frac{V_{max}}{\sqrt{2}}}\]
Signal sinusoïdal redressé - simple alternance:
Pour un signal redressé, seule la valeur positive du signal est retenue:
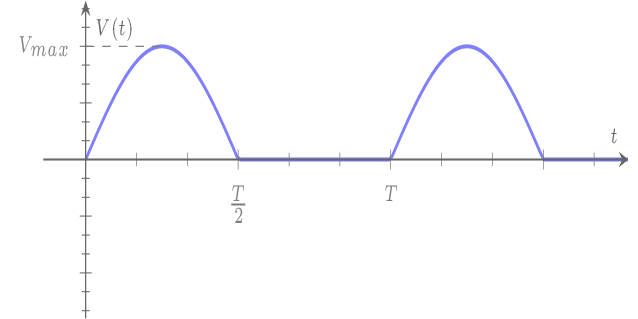
Valeur moyenne de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{\overline{V}=\frac{1}{T}\int_{0}^{T}V_{max}sin(ωt)dt\;=\;\frac{V_{max}}{π}}}\]
On peut retrouver ce résultat par calcul:
On pose θ = ωt; lorsque t varie de 0 à T, θ varie de 0 à 2π.
\[\mathsf{\overline{V}=\frac{1}{2π}\int_{0}^{2π}V_{max}sin(θ)dθ}\]
\[\mathsf{=\frac{1}{2π}\int_{0}^{π}V_{max}sin(θ)dθ + \underbrace{\frac{1}{2π}\int_{π}^{2π}V_{max}sin(θ)dθ}_{=\;0\text{; simple alternance}}}\]
\[\mathsf{=\frac{1}{2π}\int_{0}^{π}V_{max}sin(θ)dθ}\]
soit:
\[\mathsf{=\frac{1}{2π}\left[-V_{max}cos(θ)\right]_{0}^{π}}\]
finalement:
\[\mathsf{\overline{V}=\frac{V_{max}}{\pi}}\]
Valeur efficace de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=\sqrt{\frac{1}{T}\large{\int_{0}^{T}V_{max}^2sin^2(ωt)dt}}=\frac{V_{max}}{2}}}\]
On peut retrouver ce résultat à l'aide des calculs
\[\mathsf{V_{RMS}^2=\frac{1}{T}\int_{0}^{T}V_{max}^2sin^2(ωt)dt}\]
De T/2 à T, V(t) = 0.
\[\mathsf{V_{RMS}^2=\frac{1}{T}\int_{0}^{T/2}V_{max}^2sin^2(ωt)dt}\]
On pose θ = ωt; lorsque t varie de 0 à T, θ varie de 0 à 2π.
\[\mathsf{V_{RMS}^2=\frac{1}{2π}\int_{0}^{π}V_{max}^2sin^2θdθ = \frac{V_{max}^2}{2π}\left[\frac{1}{2}\left(θ-\frac{1}{2}sin(2θ)\right) \right]_{0}^{π}}\]
\[\mathsf{=\frac{V_{max}^2}{4π}[π-0] = \frac{V_{max}^2}{4}}\]
\[\mathsf{V_{RMS}=\sqrt{\frac{V_{max}^2}{4}}=\frac{V_{max}}{2}}\]
Signal sinusoïdal redressé - double alternance:
Le signal V(t) est périodique de période T/2.
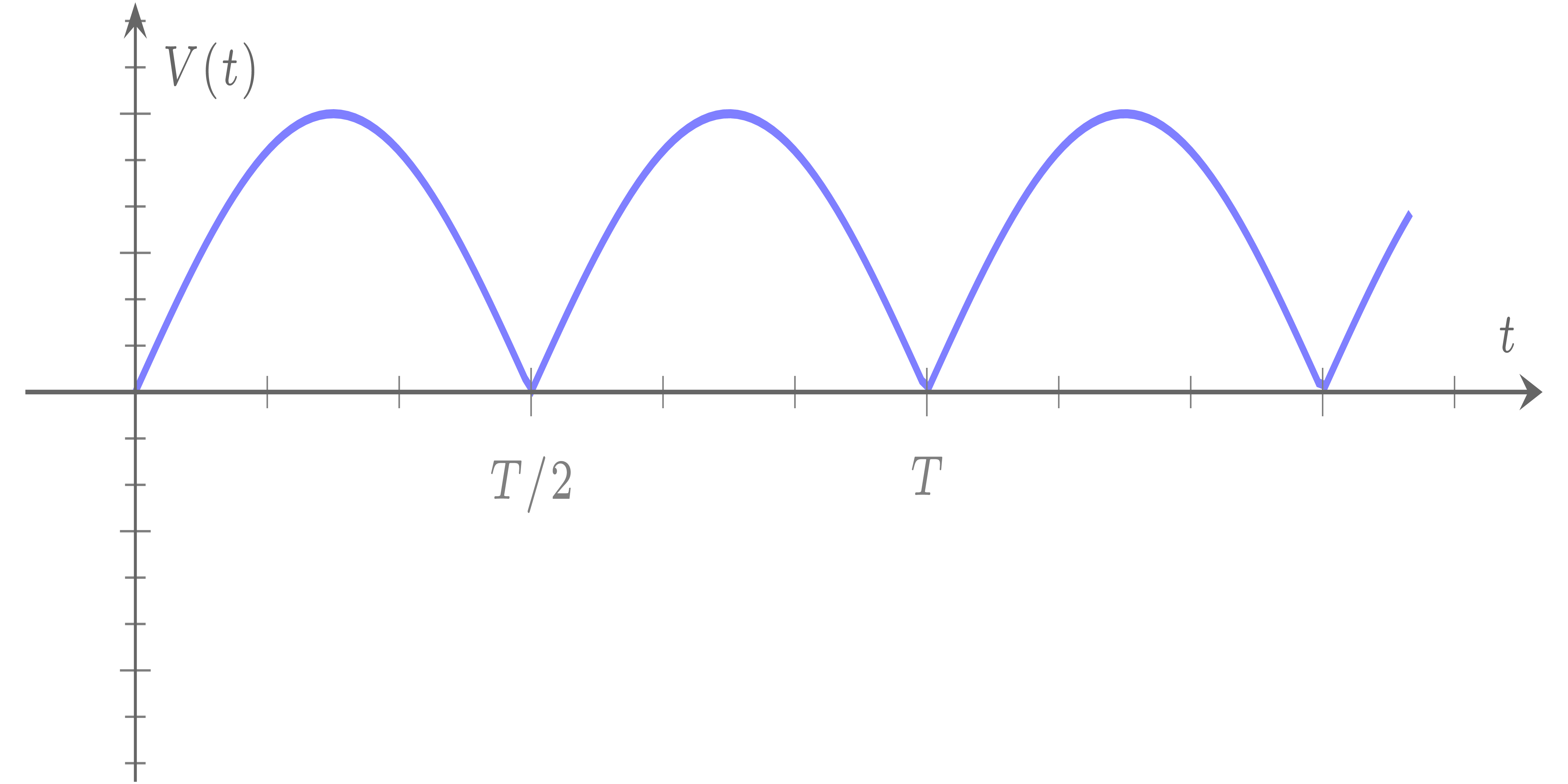
Valeur moyenne de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{\overline{V}=\frac{1}{T/2}\int_{0}^{T/2}V_{max}sin(ωt)dt = \frac{2V_{max}}{π}}}\]
On peut retrouver le résultat par calcul
En posant θ = ωt, lorsque t varie de 0 à T/2, θ varie de 0 à π; on peut écrire:
\[\mathsf{\overline{V}=\frac{1}{π}\int_{0}^{π}V_{max}sinθdθ}\]
\[\mathsf{=\frac{V_{max}}{π}[-cosθ]_{0}^{π} = \frac{2V_{max}}{π}}\]
Valeur efficace de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=\sqrt{\frac{1}{T/2}\large{\int_{0}^{T/2}V_{max}^2sin^2(ωt)dt}}=\frac{V_{max}}{\sqrt{2}}}}\]
On peut retrouver le résultat par calcul
si on pose θ = ωt, lorsque t varie de 0 à T/2, θ varie de 0 à π; on peut écrire:
\[\mathsf{V_{RMS}^2=\frac{1}{π}\int_{0}^{π}V_{max}^2sin^2θdθ}\]
\[\mathsf{V_{RMS}^2=\frac{V_{max}^2}{π}\left[\frac{1}{2}\left(θ - \frac{1}{2}sin(2θ)\right) \right]_{0}^{π} = \frac{V_{max}^2}{2π}[π-0-0]}\]
\[\mathsf{V_{RMS}=\frac{V_{max}}{\sqrt{2}}}\]
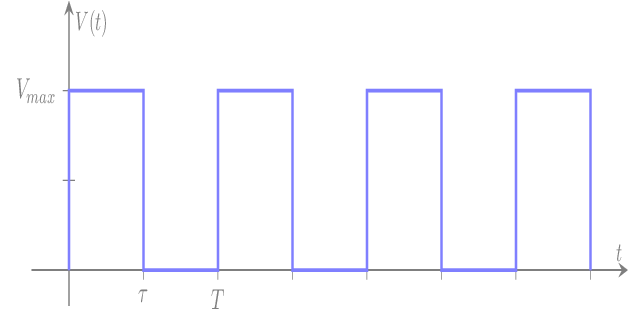
Signal carré:
Dans sa période T, le signal carré ou rectangle est définit de la façon suivante:
\(\mathsf{V(t)=\begin{cases} V_{max},&\text{ 0 < t < τ}\\0,&\text{ τ < t < T}\end{cases}}\)
Valeur moyenne de V(t):
Pour calculer la valeur moyenne il est plus simple de passer par l'aire.
Ainsi:
\[\bbox[5px,border:1px solid]{\mathsf{\overline{V}=\frac{V_{max}\tau}{T}}}\]
Valeur efficace de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=V_{max}\sqrt{\frac{\tau}{T}}}}\]
On peut aussi retrouver ce résultat par calcul.
\[\mathsf{V_{RMS}^2=\frac{1}{T}\int_{0}^{\tau}V_{max}^2dt =\frac{ V_{max}^2}{T}[t]_{0}^{\tau}=V_{max}^2\frac{\tau}{T}}\]
\[\mathsf{=V_{max}\sqrt{\frac{\tau}{T}}}\]
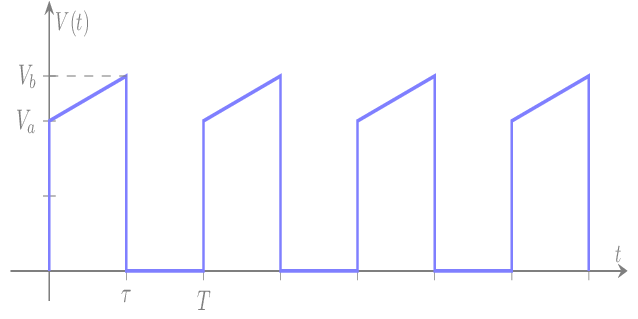
Signal trapèze:
Le signal périodique "trapèze" est définit dans sa période T par:
\(\mathsf{V(t)=\begin{cases} \large{\frac{V_b-V_a}{\tau}}t+V_a,&\text{ 0 < t < τ}\\0,&\text{ τ < t < T}\end{cases}}\)
Valeur moyenne de V(t):
Il est plus simple d'utiliser la méthode de l'aire:
Ainsi, \(\mathsf{\overline{V}=\large{\frac{\text{aire de la figure}}{T}}}\).
\[\bbox[5px,border:1px solid]{\mathsf{\overline{V}=\frac{\tau}{2T}(V_a+V_b)}}\]
Valeur efficace de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=\sqrt{\frac{\tau}{3T}(V_a^2+V_aV_b+V_b^2)}}}\]
On peut retrouver ce résultat à l'aide du calcul
\[\mathsf{V_{RMS}^2=\frac{1}{T}\int_{0}^{\tau}\left(\frac{V_b - V_a}{\tau}t+V_a \right)^2dt}\]
\[\mathsf{=\frac{1}{T}\left[\int_{0}^{\tau}\left(\frac{V_b-V_a}{\tau}\right)^2t^2dt + \int_{0}^{\tau}2\left(\frac{V_b-V_a}{\tau} \right)V_atdt+\int_{0}^{\tau}V_a^2dt\right]}\]
\[\mathsf{=\frac{1}{T}\left[\left( \frac{(V_b-V_a)^2}{\tau^2}\right).\frac{t^3}{3}+2\left(\frac{(V_b-V_a)V_a}{\tau}\right)\frac{t^2}{2}+V_a^2t \right]_{0}^{\tau}}\]
En remplaçant les bornes 0 et \(\tau\) dans l'expression précédente, on obtient après simplification des termes:
\[\mathsf{=\frac{\tau}{T}\left[\frac{(V_b-V_a)^2}{3}+(V_b-V_a)V_a + V_a^2 \right]}\]
\[\mathsf{=\frac{\tau}{3T}(V_a^2+V_aV_b+V_b^2)}\]
\[\mathsf{V_{RMS}=\sqrt{\frac{\tau}{3T}(V_a^2+V_aV_b+V_b^2)}}\]
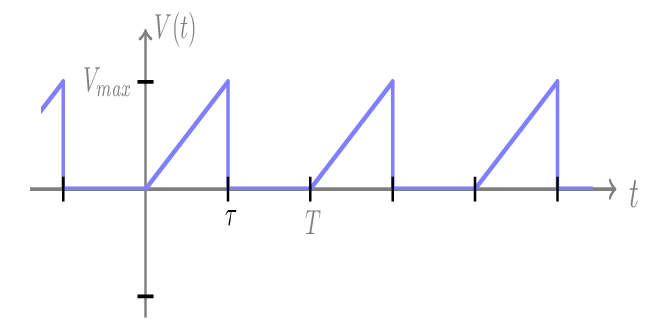
Signal dent de scie:
Sur la période T le signal dent de scie est définit par:
\(\mathsf{V(t)=\begin{cases} \large{\frac{V_{max}}{\tau}}t,&\text{ 0 < t < τ}\\0,&\text{ τ < t < T}\end{cases}}\)
Valeur moyenne de V(t):
Il est plus intéressant d'utiliser la méthode de l'aire.
Comme dans le cas des autres figures (carré et trapèze), la valeur moyenne = l'aire de la figure divisée par la période T.
La dent de scie est un triangle durant la période T.
\[\bbox[5px,border:1px solid]{\mathsf{\overline{V}=\frac{\tau}{2T}V_{max}}}\]
Valeur efficace de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=V_{max}\sqrt{\frac{\tau}{3T}}}}\]
On peut retrouver ce résultat par calcul:
\[\mathsf{V_{RMS}^2=\frac{1}{T}\int_{0}^{\tau}[V(t)]^2dt =\frac{1}{T}\int_{0}^{\tau}\left( \frac{V_{max}}{\tau}\right)^2t^2dt }\]
\[\mathsf{=\frac{1}{T}.\frac{V_{max}^2}{3}[t^3]_{0}^{\tau}}\]
\[\mathsf{V_{RMS}^2=V_{max}^2\frac{\tau}{3T}}\]
\[\mathsf{V_{RMS}=V_{max}\sqrt{\frac{\tau}{3T}}}\]
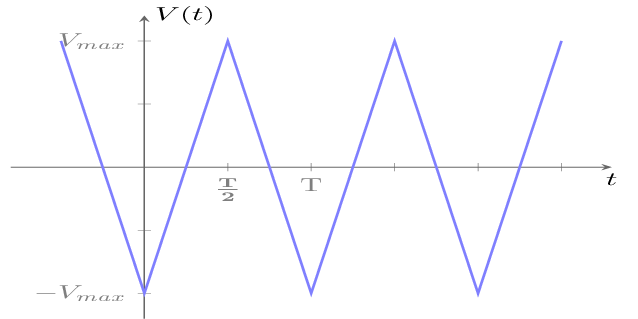
Signal triangulaire:
Sur la période T, le signal triangulaire peut se mettre sous la forme:
\(\mathsf{V(t)=\begin{cases} V_{max}\left(\frac{4}{T}t-1\right),&\text{ 0 < t < T/2}\\-V_{max}\left(\frac{4}{T}t-3\right),&\text{ T/2 < t < T}\end{cases}}\)
Valeur moyenne V(t):
On peut utiliser la méthode de l'aire pour calculer la valeur moyenne:
\[\bbox[5px,border:1px solid]{\mathsf{\overline{V}=0}}\]
Valeur efficace de V(t):
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=\frac{V_{max}}{\sqrt{3}}}}\]
On peut retrouver ce résultat par calcul
\[\mathsf{V_{RMS}^2=\frac{1}{T}\int_{0}^{T}[V(t)]^2dt}\]
\[\mathsf{=\frac{1}{T}\int_{0}^{T/2}V_{max}^2\left(\frac{4}{T}t-1\right)^2dt + \frac{1}{T}\int_{T/2}^{T}(-V_{max})^2\left(\frac{4}{T}t-3\right)^2dt}\]
\[\mathsf{=\frac{V_{max}^2}{T}\left[\int_{0}^{T/2}\left(\frac{4}{T}t-1\right)^2dt + \int_{T/2}^{T}\left(\frac{4}{T}t-3\right)^2dt\right]}\]
\[\mathsf{=\frac{V_{max}^2}{T}\left[\int_{0}^{T/2}\left(\frac{16}{T^2}t^2-\frac{8}{T}t+1\right)dt + \int_{T/2}^{T}\left(\frac{16}{T^2}t^2-\frac{24}{T}t+9\right)dt\right]}\]
\[\mathsf{=\frac{V_{max}^2}{T}\left(\left[\frac{16}{3T^2}t^3-\frac{8}{2T}t^2+t\right]_{0}^{T/2} + \left[\frac{16}{3T^2}t^3-\frac{24}{2T}t^2+9t\right]_{T/2}^{T}\right)}\]
\[\mathsf{=\frac{V_{max}^2}{T}\left(\left[\frac{2}{3}T-T+\frac{T}{2}\right] + \left[\frac{16}{3}T-\frac{2}{3}T-\frac{9}{2}T\right]\right)}\]
\[\mathsf{=\frac{V_{max}^2}{T}\left(\left[\frac{1}{6}T\right] + \left[\frac{1}{6}T\right]\right)}\]
\[\mathsf{=\frac{V_{max}^2}{3}}\]
\[\mathsf{V_{RMS}=\frac{V_{max}}{\sqrt{3}}}\]
Signaux particuliers:
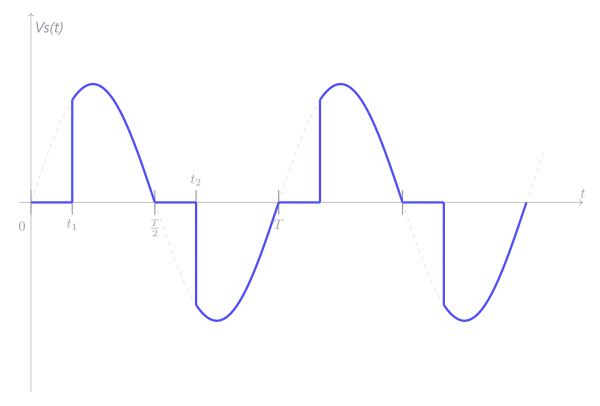
Signal de sortie d'un gradateur monophasé:
Sur la période T, ce signal peut se mettre sous la forme:
\(\mathsf{Vs(t)=\begin{cases} V_{max}sin(ωt),& t_1 < t < T/2 \text{ et }t_2 < t < T\\0,& 0 < t < t_1\text{ et } T/2 < t < t_2\end{cases}}\)
Valeur efficace de Vs(t):
\[\bbox[5px,border:1px solid]{\mathsf{V_{RMS}=\frac{V_{max}}{\sqrt{2}}\sqrt{1−\frac{α}{π}+\frac{1}{2π}sin(2α)}}}\]
\[\mathsf{V_{RMS}^2=\frac{1}{T}\int_{0}^{T}[V_s(t)]^2dt}\]
pour simplifier le calcul, on pose:
θ = ωt; α = ωt1. Lorsque t varie de 0 à T, θ varie de 0 à 2π. On peut écrire:
\[\mathsf{V_{RMS}^2=\frac{1}{2π}\int_{0}^{2π}V_{max}^2sinθ^2dθ=\frac{V_{max}^2}{2π}\int_{0}^{2π}sin^2θdθ}\]
formule de transformation:
\[\mathsf{sin^2x=\frac{1-cos(2x)}{2}}\]
donc:
\[\mathsf{V_{RMS}^2=\frac{V_{max}^2}{2π}\int_{0}^{2π}\frac{(1-cos(2θ))}{2}dθ}\]
\[\mathsf{=\frac{V_{max}^2}{4π}\left\{\int_{\alpha}^{π}(1-cos(2θ))dθ+\int_{π+\alpha}^{2π}(1-cos(2θ))dθ\right\}}\]
\[\mathsf{=\frac{V_{max}^2}{4π}\left\{\left([θ]_{α}^{π}-\frac{1}{2}[sin(2θ)]_{α}^{π}\right)+\left([θ]_{π+α}^{2π}-\frac{1}{2}[sin(2θ)]_{π+α}^{2π}\right)\right\}}\]
\[\mathsf{=\frac{V_{max}^2}{4π}[2(π-α)+sin(2α)] = \frac{V_{max}^2}{2π}[(π-α)+\frac{1}{2}sin(2α)]}\]
\[\mathsf{V_{RMS}^2=\frac{V_{max}^2}{2}(1-\frac{α}{π}+\frac{1}{2π}sin(2α)}\]
\[\mathsf{V_{RMS}=\frac{V_{max}}{\sqrt{2}}\sqrt{1−\frac{α}{π}+\frac{1}{2π}sin(2α)}}\]
Jt BB

