Les smartphones font partie intégrante de notre vie; on peut dire dans une grande part de ses aspects. En général ces précieux appareils possèdent une carte mère qui gère les différentes fonctionnalités. Dans cette carte mère, parmi les composants indispensables on trouve l'inductance, dont le rôle est d'assurer la stabilité du courant à la mise sous tension de l'appareil, de filtrer les parasites lorsqu'elle est utilisée avec d'autres composants, mais aussi de supprimer les interférences.
On trouve aussi des inductances dans les alimentations d'appareils électroniques. Elles servent aussi à lisser l'intensité du courant au démarrage des moteurs à courant continu. Les applications sont nombreuses.
Sommaire
Qu'est ce qu'une inductance?
Une inductance est une grandeur qui caractérise une bobine électrique à propriété 
magnétique. Une telle bobine est constitué d'un fil conducteur enroulé sur un support, ou tout simplement sur lui même sans support. Elle peut s'appeler solénoïde, self d'auto-induction, self de choc, ou une inductance propre.
Symbole:
Unités: le Henrys (H)
Relations fondamentales:
Loi de Faraday:
La force électromotrice induite dans un bobinage fermé placé dans un champ magnétique est proportionnelle à la variation au cours du temps du flux du champ magnétique qui entre dans le circuit:
\[\mathsf{e = -\frac{dφ}{dt}}\]
e: fem induite en volt (en V);
Le signe (–) est du à la loi de Lenz.
Le courant induit a un sens tel qu'il tend à s'opposer à la variation du flux qui l'a fait naître (loi de Lenz).
Calcul de l'inductance propre d'une bobine:
Le flux magnétique crée par une bobine est donné par:
\[\mathsf{Φ = Li}\tag{1}\label{1}\]
Φ : flux en Webers (en Wb);
L : inductance en Henrys (en H);
i : intensité du courant en Ampères (en A);
Une inductance est constituée d'un certain nombre de spires. Chaque spire balai une surface S. Soit B l'intensité de l'induction magnétique; pour une spire le flux magnétique:
\[\mathsf{φ = B.S\; \implies\;pour\, N\, spires\; Φ = N.B.S}\tag{2}\label{2}\]
N : nombre de spires
B : intensité d'induction magnétique en Tesla (T)
S : section du noyau (en \(\mathsf{m^2}\))
Soit H l'intensité du champ magnétique, dans un matériau quelconque:
\[\mathsf{B = μ.H}\tag{3}\label{3}\]
μ : perméabilité du matériau
H : en Ampères par mètres (A/m).
Pour une bobine de longueur \(\ell\), en supposant que les N spires sont jointives:
\[\mathsf{H = \frac{N.i}{\ell}}\tag{4}\label{4}\]
\(\ell\): en mètres (m)
A l'aide des formules (3) et (4), l' intensité d' induction magnétique:
\[\mathsf{B = \frac{μ_0.μ_r.N.i}{\ell}}\tag{5}\label{5}\]
µ0 : perméabilité du vide = \(\mathsf{4π.10^{-7}\; unités\;S.I.}\)
µr : perméabilité relative du matériau.
En substituant la formule (2) dans (5)
\[\mathsf{Φ = \frac{μ_0.μ_r.N^2.i.S}{\ell}}\tag{6}\label{6}\]
On peut déterminer la valeur théorique de l'inductance propre d'une bobine en posant (1) = (6):
\[\bbox[5px, border:1px solid]{\mathsf{L = \frac{μ_0.μ_r.N^2.S}{\ell}}}\]
Considérations énergétiques:
L'énergie emmagasinée dans une bobine:
\[\mathsf{E = \frac{1}{2}Li^2}\]
E : énergie en Joules (en J);
L : inductance en Henrys (en H);
i : intensité du courant en Ampères (en A);
En régime alternatif sinusoïdal, sur une période, cette énergie vaut:
\[\mathsf{E = \frac{1}{2}L{i^2}_{max}}\]
imax: intensité maximale du courant en ampères (en A).
Associations d'inductances:
On suppose que les inductances n'ont aucune influence mutuelle les unes des autres.
Montage en série:
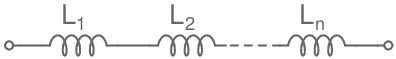
\[\bbox[5px, border:1px solid]{\mathsf{L_{eq} = L_1 + L_2 +...+ L_n}}\]
Montage en parallèle:
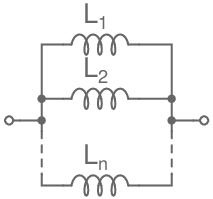
\[\bbox[5px, border:1px solid]{\mathsf{\frac{1}{L_{eq}} = \frac{1}{L_1} + \frac{1}{L_2} +...+ \frac{1}{L_n}}}\]
Bobines à noyau:
Bobines à noyau de fer:
Elles sont essentiellement utilisées en basses fréquences et dans les filtres d'alimentation.
Modèle électrique:
La puissance transmise à la bobine est en partie perdue en pertes dues au fer. Avec un wattmètre on peut mesurer une puissance active, aux bornes de la bobine cela montre l'existance d' une résistance RF liée à ces pertes. Si on ne tient pas compte de l'approximation de Kapp, le fil de cuivre constituant le bobinage présente aussi une résistance Rf. Le bobine peut être sujet à des fuites Lf; avec ceci il faudra aussi tenir compte de l'inductance principale de la bobine Lm. Cela nous donne le schéma équivalent ci-dessous:
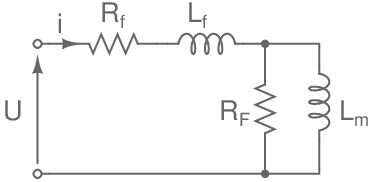
Rf : résistance du fil de cuivre constituant le bobinage (en Ω);
Lf : inductance du flux de fuite (en H);
RF : résistance représentative de l'ensemble des pertes dues au fer (en Ω);
Lm : inductance nominale de la bobine (en H).
Hypothèses de Kapp:
Si on tient compte de ces hypothèses, Rf et Lf sont négligeables.
Attention: le modèle précédent n'est qu' une approximation, Rf et Lf ne sont pas constants; ils dépendent de la fréquence d'utilisation et de la nature du matériau.
Inductance propre de la bobine à noyau de fer:
Pour déterminer l' inductance propre de la bobine à noyau de fer, on tiendra compte de l' entrefer; le noyau a une section carré.
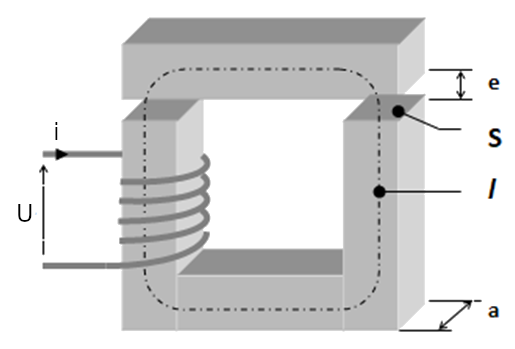
\[\mathsf{L_m = \frac{N^2}{\large{\frac{1}{μ_0}\left(\frac{1}{μ_r}.\frac{\ell}{S} + \frac{e}{S_e}\right)}}}\]
N: nombre de spires;
Lm: inductance (en H);
\(\ell\) : longueur moyenne d'une ligne de champ (en m);
S: section du noyau S = a X a (en m2);
e: épaisseur de l'entrefer;
Se: section de l'entrefer; on peut estimer par approximation que Se = S, ou alors si on veut améliorer l'estimation, prendre Se = (a + 4e)2 (en m2);
μ0: perméabilité absolue (en H/m);
μr: perméabilité relative.
Bobines à noyau ferrite:
Plage d'utilisation: des basses fréquences aux très hautes fréquences.
Modèle électrique:
Il a presque la même structure que le modèle d'une bobine à noyau fer, sauf l' apparition d'une capacité entre les spires due à l' effet de peau qui survient en haute fréquence. Celle-ci est considérée comme étant en parallèle avec l'ensemble d'une structure identique à celle de la bobine à noyau de fer:
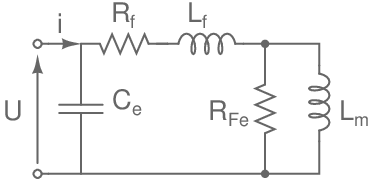
Rf: résistance du fil de cuivre constituant le bobinage;
RFe: résistance due à l'ensemble des pertes du ferrite.
Lf: inductance fuite, négligeable;
Lm : inductance nominale;
Ce: capacité entre spire valeur prépondérante aux hautes fréquences;
Pour calculer l' inductance d' une bobine à noyau de ferrite, on choisit d'abord la ferrite, puis la forme du noyau; on peut appliquer la formule
\[\mathsf{L = A_LN^2 10^9}\]
L : inductance (en H);
AL : coeffcient d'inductance, donné par le constructeur (en nH);
N : nombre de spires.
Quoi faire pour déterminer une bobine à noyau?
- Choisir le noyau, ainsi que le matériau;
- Calculer les caractéristiques.
Sont supposés connus:
Imax: courant maximal dans la bobine (en A);
L: inductance de la bobine (en H);
Bmax: induction maximale admissible par le noyau, selon le type de matériau choisi Bmax < B saturation (en T);
S: section du noyau (en m2);
\(\ell\): longueur moyenne d'une ligne de champ (en m).
Méthode de calcul possible des caractéristiques de la bobine en plusieurs étapes:
| Etapes de calcul | |
| Calculer la section de fer utile |
\(\mathsf{S_{fer} = S.k}\) k = 0.9 |
| Déterminer le flux maximal | \(\mathsf{Φ_{max}\; =\; B_{max}.S_{fer}}\) |
| Calculer le nombre de spires | \(\mathsf{N=\large{\frac{Li_{max}}{Φ_{max}}}}\) |
| Déterminer l'épaisseur de l'entrefer | \(\mathsf{e\; =\;S_e\large{(\frac{N^2 μ_0}{\ell}− \frac{1}{μ_r} \frac{\ell}{S})}}\) |
| Déterminer le diamètre des conducteurs |
\(\mathsf{d\; =\; 2.\large{\sqrt{\frac{i_{max}}{\pi.σ}}}}\) σ: densité de courant admissible dans le conducteur. |
| Réaliser la bobine | |
Bobines à noyau air:
Utilisées en hautes fréquences et en hyperfréquences, elles sont sont constituées d'un enroulement de fil rigide, bobiné sans aucun support, ou sur un support n'ayant pas de qualité magnétique (nylon, téflon, polystyrène, bakélite moulée).
Modèle électrique:
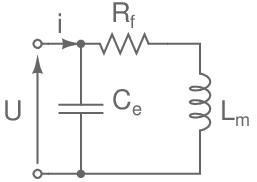
Rf : résistance du fil, dépend de l'effet de peau en HF;
Ce: capacité entre spires;
Lm: inductance nominale;
On définit aussi le facteur de qualité de la bobine:
\[\mathsf{Q = \frac{L_m ω}{R}}\]
Calcul de l'inductance propre de la bobine air une couche:
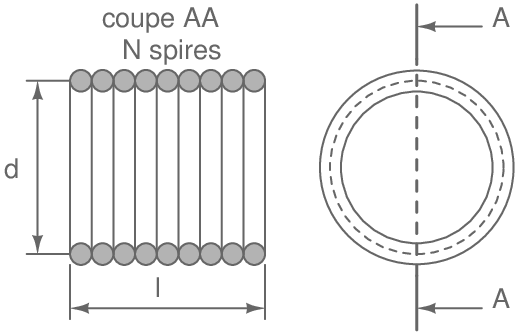
1ère méthode de calcul:
Cette méthode de calcul donne une valeur approchée qui peut être satisfaisante dans certains cas d'utilisations; elle s'applique à une bobine à spires jointives ou non.
Pour une longueur \(\ell\) de quelques mm à quelques centimètres, on peut appliquer la formule:
\[\bbox[5pix, border:1px solid]{\mathsf{L=\frac{K(πNd)^2}{1000.\ell}}}\tag{7}\label{7}\]
L : inductance propre en µH;
d : en cm
\(\ell\) : en cm
N : nombre de spires:
K : le coefficient de Hontaro Nagaoka (début 20è siècle). Les tables de Hontaro Nagaoka permettent de déterminer K en fonction du rapport \(\mathsf{\large{\frac{d}{\ell}}}\).
Dans son article sur les inductances, le merveilleux site carnets-tsf.fr a mis au goût du jour ces tables. Un exemple de calcul y est proposé. Merci pour ce travail énorme.
Une autre formule plus pratique utilise une constante K1, déduite de la constante K par:
\[\mathsf{K_1\;=\;\frac{π^2}{10}\frac{d}{\ell}K}\]
Avec d en cm, et
\(\mathsf{\ell}\) en cm.
Soit:
\[\bbox[5px, border:1px solid]{\mathsf{L =K_1\frac{N^2D}{100}}}\]
Avec L en µH.
2è méthode de calcul:
Si on ne veut pas utiliser les abaques, on peut toujours prendre une valeur approchée:
\[\mathsf{K = \frac{100}{π^2\large{\left(4\frac{d}{\ell}+11\right)}}}\tag{8}\label{8}\]
Si on remplace K expression (8) dans (7) voir la première méthode de calcul:
\[\bbox[5px,border:1px solid]{\mathsf{L(en\;µH) = \frac{N^2.d^2}{(40d + 110\ell)}}}\]
On peut utiliser cette méthode à condition d'accepter une certaine marge d'erreur.
Calcul de l' inductance propre de la bobine air multicouches:
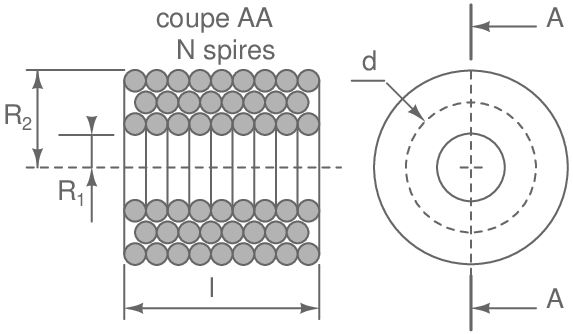
On peut utiliser deux formules pour avoir la valeur approchée de l'inductance:
Méthode empirique:
\[\bbox[5pix,border:1px solid]{\mathsf{L(en\; µH) = \frac{10πN^2R_1^2}{6R_1+9\ell + 10e}}}\]
L : inductance en µH;
N : nombre total de spires;
\(\mathsf{\ell}\) : longueur de la bobine en m;
R1 : rayon du mandrin en m;
R2 : rayon extérieur du bobinage en m;
e : épaisseur du bobinage ( e = R1 - R2) en m.
Avec une autre méthode:
\[\bbox[5px,border:1px solid]{\mathsf{L = \frac{0,08d^2N^2}{3d+9\ell+10e}}}\]
d : diamètre moyen de la bobine en cm;
\(\ell\) : longueur de la bobine en cm;
e : épaisseur du bobinage;
N : nombre de spires.
Bobine à bobinage imprimé:
Ce type de bobinage est utilisé en hyperfréquences; mais pas seulement; on peut aussi le retrouver dans des applications de communications en champ proche, comme par exemple les systèmes antidémarrage pour voitures, les télépaiements.
Forme carrée:
Exemple d'inductance imprimée:
e : l'épaisseur du cuivre;
Do : largeur extérieure en mètres;
Di : largeur intérieure en mètres;
d : espacement entre les pistes de cuivre.
Cette inductance peut être calculée par la formule:
\[\mathsf{L = 0.24bN^{\large{\frac{5}{3}}}ln\left(\frac{8b}{c}\right)}\]
L: inductance (en H);
N: nombre de spires;
b = (Do + Di)/2 (en cm);
c = (Do - Di)/2 (en cm);
Avec une autre méthode de calcul, on peut utiliser la formule améliorée de Harold A. Wheeler:
Ainsi,
\[\mathsf{L(en\;H)=K_1μ_0\left(\frac{n^2d_{avg}}{1+K_2ρ}\right)}\]
L : l'inductance en H.;
n : le nombre de spires de la bobine, (le nombre de tours);
davg : le diamètre moyen (dimension moyenne) en m.;
ρ : le taux de remplissage de la bobine, \(\mathsf{ρ=\large{\frac{Do - Di}{Do + Di}}}\);
K1 et K2 sont deux coefficients tels que:
K1 = 2,34 et K2 = 2,75 pour une forme carrée.
Forme hexagonale:
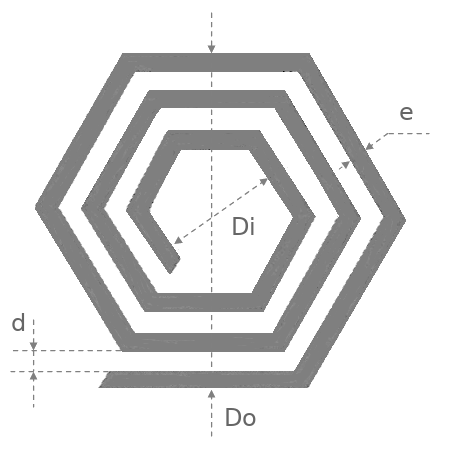Le calcul est identique à celui de la forme carrée avec la formule améliorée de Harold A. Wheeler, sauf que pour K1, on prendra 2,33 et pour K2, 3,82.
Forme octogonale:
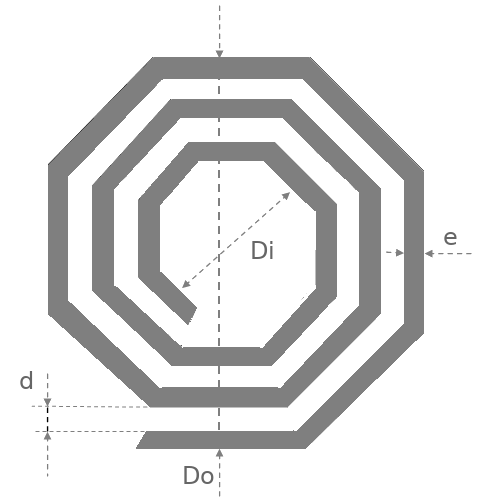
Le calcul est le même que pour la forme carrée la formule améliorée de Harold A. Wheeler, sauf que pour K1 on prendra 2,25 et pour K2, 3,55.
Forme spirale:
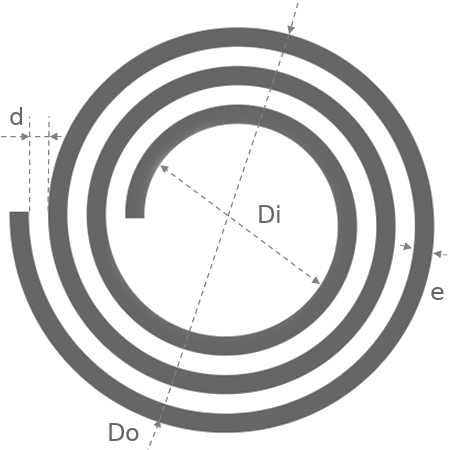
L'inductance
\[\mathsf{L(en\;H)=31,33μ_0n^2\left(\frac{a^2}{8a+11c}\right)}\]
a : le rayon moyen en m, \(\mathsf{a=\large{\frac{Di+Do}{4}}}\);
c : la largeur de la bobine en m, \(\mathsf{\large{\frac{Do-Di}{2}}}\)
μ0 = 4π×10-7 ;
Les formules de calcul pour les bobinages imprimés, proposées la méthode améliorée de Harold A. Wheeler ici ne tiennent pas compte des effets HF, ni de l'effet de peau ou des propriétés du substrat.
Elles ne sont valables uniquement que pour des fréquences basses de 120 à 150 kHz, et 13,56 MHz.
Domaines d'utilisation:
Les bobines sont utilisées pour:
- éliminer les parasites d'une alimentation électrique;
- éliminer les parasites d'un signal analogique;
- accorder un circuit en impédance;
- filtrer une bande de fréquences,
- contrôler la montée du courant continu dans les dispositifs d'électronique de puissance;
- alimenter les badges des systèmes de protection,
- alimenter les smartphones sans contact,
- etc...
Conclusion:
Les inductances sont des composants passifs très présents dans les montages électroniques; cela va des alimentations à découpages, à l'électronique de puissance en passant par les montages hautes fréquences (H.F.) ou hyperfréquences, et nos précieux smartphones. Des composants préfabriqués existent dans le commerce; mais si on a besoin d'une bobine d'inductance bien particulière, il faudra alors procéder à sa conception.
Jt BB
Ressources:
Harold A. Wheeler, "Simple inductance formulas for radio coïls", in Proc. IRE, oct 1928, vol.16, no.10, pp.1398 - 1400
The Inductances Coefficients of Solenoïds. H.Nagaoka; Journal of the College of Science, Imperial University, Tokyo, Japan. Vol XXVII, Article 6.
Fabricants: Murata, TDK,...et bien d'autres.
